题目内容
甲乙两名同学参加某种选拔测试,在相同测试条件下,两人5次测试的成绩(单位:分)如下表:
(1)请计算甲、乙两人成绩的平均数和方差,并据此判断选派谁参赛更好
(2)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,设抽到的两个成绩中,80分以上的个数为ξ,求随机变量ξ的分布列和数学期望.
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 甲 | 60 | 63 | 75 | 80 | 87 |
| 乙 | 55 | 65 | 77 | 78 | 89 |
(2)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,设抽到的两个成绩中,80分以上的个数为ξ,求随机变量ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(1)求出甲、乙两人成绩的平均数和方差,得
>
,S甲2<S乙2,从而甲的平均成绩高且方差小,故选派甲参赛更好.
(2)由已知得ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
. |
| x甲 |
. |
| x乙 |
(2)由已知得ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答:
解:(1)
=
(60+63+75+80+87)=73,
=
(55+65+77+78+89)=72.8,
S甲2=
[(60-73)2+(65-73)2+(77-73)2+(78-73)2+(89-73)2]=106,
S乙2=
[(55-72.8)2+(65-72.8)2+(77-72.8)2+(78-72.8)2+(89-72.8)2]=136.96,
∵
>
,S甲2<S乙2,
∴甲的平均成绩高且方差小,故选派甲参赛更好.
(2)由已知得ξ的可能取值为0,1,2,
P(ξ=0)=
•
=
,
P(ξ=1)=
•
+
•
=
,
P(ξ=2)=
•
=
,
∴ξ的分布列为:
Eξ=0×
+1×
+2×
=
.
. |
| x甲 |
| 1 |
| 5 |
. |
| x乙 |
| 1 |
| 5 |
S甲2=
| 1 |
| 5 |
S乙2=
| 1 |
| 5 |
∵
. |
| x甲 |
. |
| x乙 |
∴甲的平均成绩高且方差小,故选派甲参赛更好.
(2)由已知得ξ的可能取值为0,1,2,
P(ξ=0)=
| ||
|
| ||
|
| 2 |
| 25 |
P(ξ=1)=
| ||
|
| ||
|
| ||
|
| ||
|
| 11 |
| 25 |
P(ξ=2)=
| ||
|
| ||
|
| 12 |
| 25 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 2 |
| 25 |
| 11 |
| 25 |
| 12 |
| 25 |
| 7 |
| 5 |
点评:本题考查平均数和方差的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
设z=x+y,其中实数x,y满足
,则z的最大值为( )
|
| A、12 | B、6 | C、0 | D、-6 |
已知直线l⊥平面α,直线m?平面β,有下列四个命题:
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
其中,正确命题的序号是( )
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β.
其中,正确命题的序号是( )
| A、①② | B、③④ | C、①③ | D、②④ |
已知双曲线C:
-
=1的焦距为10,点P(1,2)在C的渐近线上,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
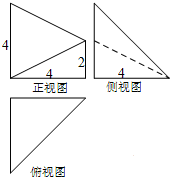 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V=