题目内容
函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
| A、13 | ||
| B、2 | ||
C、
| ||
D、
|
考点:函数的值
专题:函数的性质及应用
分析:由已知得f(x+2)=
,从而f(99)=
=f(95)=
=f(91)=
=f(87)=f(3)=
=
.
| 13 |
| f(x) |
| 13 |
| f(97) |
| 13 |
| f(93) |
| 13 |
| f(89) |
| 13 |
| f(1) |
| 13 |
| 2 |
解答:
解:∵函数f(x)满足f(x)•f(x+2)=13,f(1)=2,
∴f(x+2)=
,
∴f(99)=
=f(95)=
=f(91)
=
=f(87)=f(3)=
=
.
故选:D.
∴f(x+2)=
| 13 |
| f(x) |
∴f(99)=
| 13 |
| f(97) |
| 13 |
| f(93) |
=
| 13 |
| f(89) |
| 13 |
| f(1) |
| 13 |
| 2 |
故选:D.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数的周期性的合理运用.

练习册系列答案
相关题目
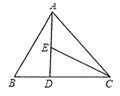 如图所示,在△ABC中,
如图所示,在△ABC中,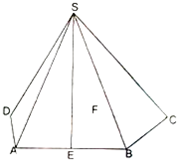 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.