题目内容
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}前n项和,则log2(S2012+2)= .
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:依题意,a1=2且an+an-1=2n+2n-1,则S2012=(a1+a2)+(a3+a4)+…+(a2011+a2012),利用等比数列的求和公式可求得S2012+2=22013,从而可得答案.
解答:
解:∵an+an-1=2n+2n-1,Sn为数列{an}前n项和,
∴S2012=(a1+a2)+(a3+a4)+…+(a2011+a2012)
=(21+22)+(23+2?)+…+(22011+22012)
=2+22+23+…+22012
=
=22013-2,
∴S2012+2=22013,
∴log2(S2012+2)=log222013=2013.
故答案为:2013.
∴S2012=(a1+a2)+(a3+a4)+…+(a2011+a2012)
=(21+22)+(23+2?)+…+(22011+22012)
=2+22+23+…+22012
=
| 2(1-22012) |
| 1-2 |
∴S2012+2=22013,
∴log2(S2012+2)=log222013=2013.
故答案为:2013.
点评:本题考查数列的求和,依题意得到S2012=(a1+a2)+(a3+a4)+…+(a2011+a2012)是关键,考查化归思想与等比数列的求和及对数的运算性质,属于中档题.

练习册系列答案
相关题目
已知A、B两地相距150km,某人开汽车以60km/h的速度从A到达B地,在B地停留一小时后再以50km/h的速度返回A地,将汽车离开A地的距离y表示为时间t的函数,其函数表达式为( )
| A、y=60t | |||||||||
B、y=
| |||||||||
| C、y=60t+50t | |||||||||
D、y=
|
为了弘扬孝道感恩的美德,某学校准备组织一批学生观看亲情励志电影《孝女彩金》.现有10张《孝女彩金》的电影票分给6个班的学生去观看,每个班至少分一张电影票,则不同的分法有( )种.
| A、60 | B、64 |
| C、126 | D、253 |
 一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )
一个底面是直角梯形的四棱锥的三视图如图所示,则此四棱锥的四个侧面的面积和为( )A、
| ||||||||
B、3
| ||||||||
C、3
| ||||||||
D、
|
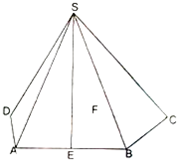 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.