题目内容
设集合A={x|
<2x<4},B={x|x2≤1},则A∪B=( )
| 1 |
| 2 |
| A、{x|x<2} | ||
B、{x|-
| ||
| C、{x|-1≤x<2} | ||
| D、{x|1≤x<2} |
考点:并集及其运算
专题:集合
分析:利用并集的性质求解.
解答:
解:∵集合A={x|
<2x<4}={}x|-1<x<2},
B={x|x2≤1}={x|-1≤x≤1},
∴A∪B={x|-1≤x<2}.
故选:C.
| 1 |
| 2 |
B={x|x2≤1}={x|-1≤x≤1},
∴A∪B={x|-1≤x<2}.
故选:C.
点评:本题考查并集的求法,是基础题,解题时要注意不等式性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A、B两地相距150km,某人开汽车以60km/h的速度从A到达B地,在B地停留一小时后再以50km/h的速度返回A地,将汽车离开A地的距离y表示为时间t的函数,其函数表达式为( )
| A、y=60t | |||||||||
B、y=
| |||||||||
| C、y=60t+50t | |||||||||
D、y=
|
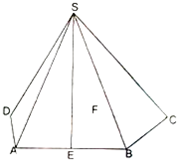 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点. 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右各小长方形的面积之比为1:3:4:2,第四小组频数为10.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右各小长方形的面积之比为1:3:4:2,第四小组频数为10.