题目内容
定义:若数列{An}满足An+1=An2,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=2,点(an,an+1)在函数f(x)=2x2+2x的图象上,其中n为正整数.
(1)证明:数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;
(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)•…•(2an+1),求数列{an}的通项及Tn的表达式.
(1)证明:数列{2an+1}是“平方递推数列”,且数列{lg(2an+1)}为等比数列;
(2)设(1)中“平方递推数列”的前n项之积为Tn,即Tn=(2a1+1)(2a2+1)•…•(2an+1),求数列{an}的通项及Tn的表达式.
考点:数列的求和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)依题意,可得2an+1+1=4an2+4an+1=(2an+1)2,依新定义可证数列{2an+1}是“平方递推数列”,继而可证
=2,数列{lg(2an+1)}为等比数列;
(2)由(1)知数列{lg(2an+1)}为等比数列,从而可得lg(2an+1)=2n-1•lg5=lg52n-1,易求数列{an}的通项;再由lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)=
=(2n-1)lg5=lg52n-1,即可求得Tn的表达式.
| lg(2an+1+1) |
| lg(2an+1) |
(2)由(1)知数列{lg(2an+1)}为等比数列,从而可得lg(2an+1)=2n-1•lg5=lg52n-1,易求数列{an}的通项;再由lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)=
| (1-2n)•lg5 |
| 1-2 |
解答:
(1)证明:由条件得an+1=2an2+2an.
∴2an+1+1=4an2+4an+1=(2an+1)2.
∴数列{2an+1}是“平方递推数列”.
由a1=2及2an+1+1=(2an+1)2,
知2an+1>1恒成立,且lg(2an+1+1)=2lg(2an+1),
∴
=2.
∴数列{lg(2an+1)}为等比数列.
(2)解:∵a1=2,∴lg(2a1+1)=lg5,
∴lg(2an+1)=2n-1•lg5=lg52n-1,
∴2an+1=52n-1.
∴an=
(52n-1-1).
∵lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)
=
=(2n-1)lg5=lg52n-1,
∴Tn=52n-1.
∴2an+1+1=4an2+4an+1=(2an+1)2.
∴数列{2an+1}是“平方递推数列”.
由a1=2及2an+1+1=(2an+1)2,
知2an+1>1恒成立,且lg(2an+1+1)=2lg(2an+1),
∴
| lg(2an+1+1) |
| lg(2an+1) |
∴数列{lg(2an+1)}为等比数列.
(2)解:∵a1=2,∴lg(2a1+1)=lg5,
∴lg(2an+1)=2n-1•lg5=lg52n-1,
∴2an+1=52n-1.
∴an=
| 1 |
| 2 |
∵lgTn=lg(2a1+1)+lg(2a2+1)+…+lg(2an+1)
=
| (1-2n)•lg5 |
| 1-2 |
∴Tn=52n-1.
点评:本题考查数列的求和,考查等比关系的确定及等比数列通项公式与求和公式的综合应用,考查推理运算能力,属于难题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
已知A、B两地相距150km,某人开汽车以60km/h的速度从A到达B地,在B地停留一小时后再以50km/h的速度返回A地,将汽车离开A地的距离y表示为时间t的函数,其函数表达式为( )
| A、y=60t | |||||||||
B、y=
| |||||||||
| C、y=60t+50t | |||||||||
D、y=
|
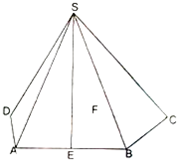 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点. 为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右各小长方形的面积之比为1:3:4:2,第四小组频数为10.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右各小长方形的面积之比为1:3:4:2,第四小组频数为10.