题目内容
已知函数f(x)=sin2x-2sin2x
(1)求函数f(x)的最小正周期.
(2)求函数单调递增区间.
(3)求函数f(x)的最大值及f(x)取最大值时x的集合.
(1)求函数f(x)的最小正周期.
(2)求函数单调递增区间.
(3)求函数f(x)的最大值及f(x)取最大值时x的集合.
考点:三角函数的最值,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)首先通过恒等变换把函数变换成正弦型函数,进一步求出最小正周期.
(2)利用整体思想求出单调增区间.
(3)利用整体死刑进一步求出函数的最值.
(2)利用整体思想求出单调增区间.
(3)利用整体死刑进一步求出函数的最值.
解答:
解:(1)函数f(x)=sin2x-2sin2x=sin2x+cos2x-1=
sin(2x+
)-1
则:T=π
(2)函数f(x)=
sin(2x+
)-1
则函数的单调递增区间:令2kπ-
≤2x+
≤2kπ+
(k∈Z)
解得:kπ-
≤x≤kπ+
(k∈Z)
故单调递增区间为:[kπ-
,kπ+
](k∈Z)
(3)当2x+
=2kπ+
时,即:x=kπ+
时,f(x)max=
+1
当2x+
=2kπ-
时,即:x=kπ-
时,f(x)min=-
+1
故答案为:(1)T=π
(2)故单调递增区间为:[kπ-
,kπ+
](k∈Z)
(3)当2x+
=2kπ+
时,即:x=kπ+
时,f(x)max=
+1
当2x+
=2kπ-
时,即:x=kπ-
时,f(x)min=-
+1
| 2 |
| π |
| 4 |
则:T=π
(2)函数f(x)=
| 2 |
| π |
| 4 |
则函数的单调递增区间:令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得:kπ-
| 3π |
| 8 |
| π |
| 8 |
故单调递增区间为:[kπ-
| 3π |
| 8 |
| π |
| 8 |
(3)当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
当2x+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| 2 |
故答案为:(1)T=π
(2)故单调递增区间为:[kπ-
| 3π |
| 8 |
| π |
| 8 |
(3)当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
当2x+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| 2 |
点评:本题考查的知识要点:三角函数的恒等变换,正弦型函数的最小正周期,正弦型函数的单调区间及最值

练习册系列答案
相关题目
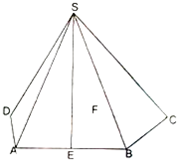 在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.
在四棱锥S-ABCD中,已知AB∥CD,SA=SB,SC=SD,E,F分别为AB,CD的中点.