题目内容

设an是（x+3）n的展开式中x的一次项的系数，则（
32
a2
+
33
a3
+…+
32008
a2008
）的值为
 
．
考点：二项式定理的应用
专题：二项式定理
分析：由题意可得an=
C
n-1
n
•3n-1=n•3n-1，
3n
an
=
n
3
，再根据
32
a2
+
33
a3
+…+
32008
a2008
=
2
3
+
3
3
+
4
3
+…+
2008
3
，利用等差数列的求和公式，计算求得结果．
解答： 解：由于an是（x+3）n的展开式中x的一次项的系数，故an=
C
n-1
n
•3n-1=n•3n-1，∴
3n
an
=
n
3
，
则（
32
a2
+
33
a3
+…+
32008
a2008
）=
2
3
+
3
3
+
4
3
+…+
2008
3
=
2+3+4+…+2008
3
=
2007(2+2008)
2
3
=2007×335=673005，
故答案为：673005．
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，等差数列的求和公式，属于基础题．
练习册系列答案
相关题目
将87化成二进制数为（　　）
A、1010111（2）
B、1010110（2）
C、1110101（2）
D、1010101（2）
设f（x）=
1
x+2
+log
1-x
1+x
的反函数是y=g（x），求方程g（x）=
9
11
解集．
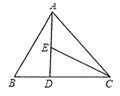如图所示，在△ABC中，
BD
=
1
2
DC
，
AE
=3
ED
，若
AB
=
a
，
AC
=
b
，则
CE
=
 
．
[x]表示不超过x的最大整数，则f（x）=x3-[x]的零点集合是
 
．
已知函数f（x）=
1
x+1
+log3
2-x
x
．
（1）求f（x）的定义域；
（2）判断f（x）的单调性并证明；
（3）x取何值时，f[x（x-
1
2
）]＞
1
2
？
已知函数f（x）=2（sin4x+cos4x）+m（sinx+cosx）4在x∈[0，
π
2
）上的最大值为5，求实数m的值．
已知函数f（x）是（0，+∞）上的非常值函数，对任意x，y∈R，满足f（xy）=f（x）+f（y），且0＜x＜1时，f（x）＜0．
（1）求f（1）；
（2）求证：f（x）在（0，+∞）上为增函数
（3）若f（3）=1，且f（a）＞f（a-1）+2，求a的取值范围．
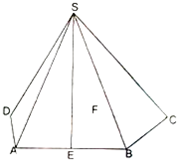在四棱锥S-ABCD中，已知AB∥CD，SA=SB，SC=SD，E，F分别为AB，CD的中点．
（1）求证：平面SEF⊥平面ABCD；
（2）若平面SAB∩平面SCD=l，试问l与平面ABCD是否平行，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网