题目内容
16.若命题p:?x0∈R,x0-2>lgx0,则¬p是( )| A. | ?x0∈R,x0-2≤lgx0 | B. | ?x0∈R,x0-2<lgx0 | C. | ?x∈R,x-2<lgx | D. | ?x∈R,x-2≤lgx |
分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以,命题p:?x0∈R,x0-2>lgx0,则¬p是?x0∈R,x0-2≤lgx0.
故选:A.
点评 本题考查命题的否定特称命题与全称命题的否定关系,是基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
7.已知集合A={x|2x≤1,x∈R},B={a,1},若A∩B≠∅,则实数a的取值范围是( )
| A. | a<1 | B. | a≤1 | C. | a≥0 | D. | a≤0 |
1.过点P(1,2)的直线与圆x2+y2=4相切,且与直线ax-y+1=0垂直,则实数a的值为( )
| A. | 0 | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 0或$\frac{3}{4}$ |
8.“函数f(x)=x3+(a2-1)x2为奇函数”是“a=1”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
6.直线y=x+m与圆C:(x+4)2+y2=8交于M、N两点,且|$\overrightarrow{MN}$|≥$\sqrt{3}$|$\overrightarrow{CM}$+$\overrightarrow{CN}$|,则实数m的取值范围是( )
| A. | [2,6] | B. | [4-$\sqrt{2}$,4+$\sqrt{2}$] | C. | [-6,-2] | D. | [-4-$\sqrt{2}$,-4+$\sqrt{2}$] |
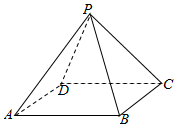 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.