题目内容
1.过点P(1,2)的直线与圆x2+y2=4相切,且与直线ax-y+1=0垂直,则实数a的值为( )| A. | 0 | B. | -$\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 0或$\frac{3}{4}$ |
分析 由题意画出图形,求出圆的切线方程,再由切线与直线ax-y+1=0垂直求得a值.
解答 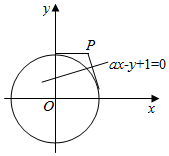 解:如图,
解:如图,
由图可知,过点P(1,2)与圆x2+y2=4相切的直线有两条,
设为y-2=k(x-1),即kx-y-k+2=0,
由$\frac{|-k+2|}{\sqrt{{k}^{2}+1}}=2$,解得k=0或k=-$\frac{4}{3}$,
当k=0时,不与直线ax-y+1=0垂直,
当k=-$\frac{4}{3}$时,若与直线ax-y+1=0垂直,则a=$\frac{3}{4}$.
故选:C.
点评 本题考查圆的切线方程,训练了点到直线距离公式的应用,体现了分类讨论与数形结合的解题思想方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若命题p:?x0∈R,x0-2>lgx0,则¬p是( )
| A. | ?x0∈R,x0-2≤lgx0 | B. | ?x0∈R,x0-2<lgx0 | C. | ?x∈R,x-2<lgx | D. | ?x∈R,x-2≤lgx |
6.若z=i(1+i),则|z|等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
13.设函数f(x)=kx+b,若f(1)=-2,f(-1)=0,则( )
| A. | k=1,b=-1 | B. | k=-1,b=-1 | C. | k=-1,b=1 | D. | k=1,b=1 |
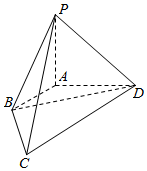 如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$.
如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$.