题目内容
11.已知a+2b=1且b>1,则$\frac{1}{a}$+$\frac{a}{b}$的取值范围是(-2,1-2$\sqrt{2}$].分析 化简$\frac{1}{a}$+$\frac{a}{b}$=$\frac{1}{1-2b}$+$\frac{1}{b}$-2,再令f(x)=$\frac{1}{1-2x}$+$\frac{1}{x}$-2,x>1;从而求导判断函数的单调性,从而求取值范围.
解答 解:∵a+2b=1且b>1,
∴a=1-2b,
$\frac{1}{a}$+$\frac{a}{b}$=$\frac{1}{1-2b}$+$\frac{1-2b}{b}$=$\frac{1}{1-2b}$+$\frac{1}{b}$-2,
令f(x)=$\frac{1}{1-2x}$+$\frac{1}{x}$-2,x>1;
则f′(x)=$\frac{2}{(1-2x)^{2}}$-$\frac{1}{{x}^{2}}$=($\frac{\sqrt{2}}{1-2x}$+$\frac{1}{x}$)($\frac{\sqrt{2}}{1-2x}$-$\frac{1}{x}$),
=($\frac{1}{x}$+$\frac{\sqrt{2}}{2x-1}$)$\frac{1-(2-\sqrt{2})x}{x(2x-1)}$,
又∵x>1,
∴$\frac{1}{x}$+$\frac{\sqrt{2}}{2x-1}$>0,x(2x-1)>0;
∴当1-(2-$\sqrt{2}$)x>0,即1<x<$\frac{2+\sqrt{2}}{2}$时,f(x)为增函数;
当1-(2-$\sqrt{2}$)x<0,即x>$\frac{2+\sqrt{2}}{2}$时,f(x)为减函数;
且$\underset{lim}{x→1}$f(x)=-2,f($\frac{2+\sqrt{2}}{2}$)=1-2$\sqrt{2}$,$\underset{lim}{x→+∞}$f(x)=-2,
故-2<f(x)≤1-2$\sqrt{2}$;
故$\frac{1}{a}$+$\frac{a}{b}$的取值范围是(-2,1-2$\sqrt{2}$];
故答案为:(-2,1-2$\sqrt{2}$].
点评 本题考查了导数的综合应用及极限的定义的应用,同时考查了转化思想的应用及整体思想的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| 单价x(单位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(单位:万件) | 90 | 84 | 83 | 80 | 75 | 68 |
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入-成本)
| A. | (0,1] | B. | [1,2) | C. | [-2,2) | D. | (0,2) |
| A. | ?x0∈R,x0-2≤lgx0 | B. | ?x0∈R,x0-2<lgx0 | C. | ?x∈R,x-2<lgx | D. | ?x∈R,x-2≤lgx |
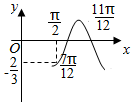 已知函数f(x)=Acos(ωx+φ)的图象如图所示,则f($\frac{5π}{6}$)=( )
已知函数f(x)=Acos(ωx+φ)的图象如图所示,则f($\frac{5π}{6}$)=( )| A. | -$\frac{2}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | -3 | B. | 4 | C. | 3 | D. | -11 |