题目内容
8．“函数f（x）=x3+（a2-1）x2为奇函数”是“a=1”的（ ）| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 由函数f（x）=x3+（a2-1）x2为奇函数，可得f（-x）+f（x）=0，解出a即可判断出结论．
解答 解：∵函数f（x）=x3+（a2-1）x2为奇函数，
∴f（-x）+f（x）=0，可得a2-1=0，解得a=±1，
∴“函数f（x）=x3+（a2-1）x2为奇函数”是“a=1”的必要不充分条件．
故选：A．
点评 本题考查了函数的奇偶性、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
有一个可同时进出水的容器，每单位时间内的水量是一定的，设从某时刻开始10min内只进水不出水，在随后的30min内既进水又出水，得到时间x（min）与水量y（L）之间的关系如图所示．若40min后只放水不进水，求y与x的函数关系．
16．若命题p：?x0∈R，x0-2＞lgx0，则￢p是（ ）
| A． | ?x0∈R，x0-2≤lgx0 | B． | ?x0∈R，x0-2＜lgx0 | C． | ?x∈R，x-2＜lgx | D． | ?x∈R，x-2≤lgx |
3．
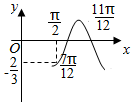已知函数f（x）=Acos（ωx+φ）的图象如图所示，则f（$\frac{5π}{6}$）=（ ）
已知函数f（x）=Acos（ωx+φ）的图象如图所示，则f（$\frac{5π}{6}$）=（ ）| A． | -$\frac{2}{3}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
13．设函数f（x）=kx+b，若f（1）=-2，f（-1）=0，则（ ）
| A． | k=1，b=-1 | B． | k=-1，b=-1 | C． | k=-1，b=1 | D． | k=1，b=1 |