题目内容
6.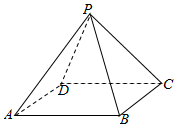 如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
如图,正四棱锥P-ABCD的底面一边AB长为$2\sqrt{3}cm$,侧面积为$8\sqrt{3}c{m^2}$,则它的体积为4.
分析 作出棱锥的高PO,则O为底面中心,作OE⊥AB于E,根据侧面积计算PE,利用勾股定理计算PO,带入体积公式计算体积.
解答 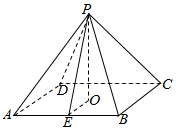 解:过P作底面ABCD的垂线PO,则O为底面正方形ABCD的中心,
解:过P作底面ABCD的垂线PO,则O为底面正方形ABCD的中心,
过O作OE⊥AB于E,连结PE.则OE=$\frac{1}{2}AB$=$\sqrt{3}$.
∵PO⊥平面ABCD,AB?平面ABCD,
∴PO⊥AB,
又AB⊥OB,PO?平面POE,OE?平面POE,PO∩OE=O,
∴AB⊥平面POE,∵PE?平面POE,
∴AB⊥PE.
∴正四棱锥的侧面积S侧=4S△PAB=4×$\frac{1}{2}×2\sqrt{3}×PE$=8$\sqrt{3}$,
解得PE=2.
∴PO=$\sqrt{P{E}^{2}-O{E}^{2}}$=1.
∴正四棱锥的体积V=$\frac{1}{3}$S正方形ABCD•PO=$\frac{1}{3}×$(2$\sqrt{3}$)2×1=4.
故答案为:4.
点评 本题考查了正四棱锥的结构特征,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
10.已知函数f(x)=-x+log2$\frac{1-x}{1+x}$,若方程m-e-x=f(x)在[-$\frac{1}{3}$,$\frac{1}{3}$]内有实数解,则实数m的最小值是( )
| A. | e${\;}^{-\frac{1}{3}}$+$\frac{4}{3}$ | B. | e${\;}^{\frac{1}{3}}$+$\frac{4}{3}$ | C. | e${\;}^{\frac{1}{3}}$-$\frac{4}{3}$ | D. | e${\;}^{-\frac{1}{3}}$-$\frac{4}{3}$ |
16.若命题p:?x0∈R,x0-2>lgx0,则¬p是( )
| A. | ?x0∈R,x0-2≤lgx0 | B. | ?x0∈R,x0-2<lgx0 | C. | ?x∈R,x-2<lgx | D. | ?x∈R,x-2≤lgx |
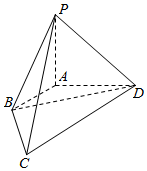 如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$.
如图,在四棱锥P-ABCD中,已知棱AB,AD,AP两两垂直,长度分别为1,2,2.若$\overrightarrow{DC}$=λ$\overrightarrow{AB}$,且向量$\overrightarrow{PC}$与$\overrightarrow{BD}$夹角的余弦值为$\frac{\sqrt{15}}{15}$. 有一个可同时进出水的容器,每单位时间内的水量是一定的,设从某时刻开始10min内只进水不出水,在随后的30min内既进水又出水,得到时间x(min)与水量y(L)之间的关系如图所示.若40min后只放水不进水,求y与x的函数关系.
有一个可同时进出水的容器,每单位时间内的水量是一定的,设从某时刻开始10min内只进水不出水,在随后的30min内既进水又出水,得到时间x(min)与水量y(L)之间的关系如图所示.若40min后只放水不进水,求y与x的函数关系.