题目内容
已知数列{an}的通项an=2ncos(nπ),则a1+a2+…+a99+a100=( )
| A、0 | ||
B、
| ||
| C、2-2101 | ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出数列{an}的通项公式an=(-2)n.由此能求出a1+a2+…+a99+a100的值.
解答:
解:∵an=2ncos(nπ),
∴a1=2•cosπ=-2,
an=2n•cos(nπ)
n为奇数时,cos(nπ)=-1,an=-2ⁿ
n为偶数时,cos(nπ)=1,an=2ⁿ,
综上,数列{an}的通项公式an=(-2)n.
∴数列{an}是以-2为首项,-2为公比的等比数列,
∴a1+a2+…+a99+a100
=
=
(2100-1).
故选:D.
∴a1=2•cosπ=-2,
an=2n•cos(nπ)
n为奇数时,cos(nπ)=-1,an=-2ⁿ
n为偶数时,cos(nπ)=1,an=2ⁿ,
综上,数列{an}的通项公式an=(-2)n.
∴数列{an}是以-2为首项,-2为公比的等比数列,
∴a1+a2+…+a99+a100
=
| (-2)×[(-2)100-1] |
| (-2-1) |
=
| 2 |
| 3 |
故选:D.
点评:本题考查数列的前100项和的求法,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
从不同号码的三双靴中任取4只,其中恰好有一双的取法种数为( )
| A、12 | B、24 | C、36 | D、72 |
设集合P={x∈R|x2+2x<0},Q={x∈R|
>0},则P∩Q=( )
| 1 |
| x+1 |
| A、(-2,1) | B、(-1,0) |
| C、∅ | D、(-2,0) |
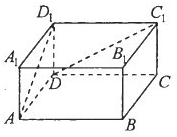 如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )
如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
一次调查男女学生喜欢语文学科情况,共调查了90人,具体如下:据此材料,你认为喜欢语文学科与性别( )
| 喜欢 | 不喜欢 | |
| 男 | 20 | 25 |
| 女 | 30 | 15 |
| A、有关 | B、无关 |
| C、不确定 | D、无法判断 |
角α的终边过P(sin
,cos
),则角α的最小正值是( )
| 2π |
| 3 |
| 2π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的渐近线方程是( )
| y2 |
| 9 |
| x2 |
| 16 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|