题目内容
从不同号码的三双靴中任取4只，其中恰好有一双的取法种数为（ ）
| A、12 | B、24 | C、36 | D、72 |
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：先从3双靴中取出1双，再从剩下的2双中任取两双，从这两双中各取1只，由分步计数原理可得．
解答：
解：先从3双靴中取出1双，有3种选法，
再从剩下的2双中任取两双，从这两双中各取1只，共有2×2=4种情况，
由分步计数原理可得，共有3×4=12种．
故选：A．
再从剩下的2双中任取两双，从这两双中各取1只，共有2×2=4种情况，
由分步计数原理可得，共有3×4=12种．
故选：A．
点评：本题考查排列组合及简单的计数问题，由分步计数原理设计选择的方案是解决问题的关键，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在数列{an}中，若a1=
，an+1=an+ln（1+
），则an等于（ ）
| 1 |
| 2 |
| 1 |
| n |
| A、2+ln n | ||
| B、2+n ln n | ||
C、
| ||
D、
|
已知命题P：?x∈（0，1），x2＜x3；命题q：若函数f（x）=ln（a+
）为奇函数，则a=-1，下列命题中真命题是（ ）
| 2 |
| x+1 |
| A、p∧q | B、p∧￢q |
| C、￢p∧q | D、￢p∧￢q |
已知数列{an}的通项公式an=-2n2+15n+2，则此数列的最大项是（ ）
| A、第1项 | B、第3项 |
| C、第4项 | D、第7项 |
下列四个函数中，能在x=0处取得极值的是（ ）
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x．
①y=x3 ②y=x2+1 ③y=cosx-1 ④y=2x．
| A、①② | B、②③ | C、③④ | D、①③ |
如图，正方形ACDE与等腰直角三角形ACB所在的平面互相垂直，且AC=BC=2，∠ACB=90°，F，G分别是线段AE，BC的中点，则AD与GF所成的角的余弦值为（ ）A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
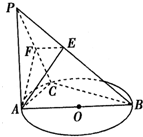如图，PA垂直于圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC，
正确命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知数列{an}的通项an=2ncos（nπ），则a1+a2+…+a99+a100=（ ）
| A、0 | ||
B、
| ||
| C、2-2101 | ||
D、
|