题目内容
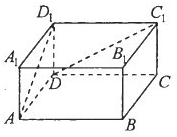 如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )
如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
考点:异面直线及其所成的角
专题:空间角
分析:连结AB1,D1B1,由AB1∥DC1,知∠D1AB1是异面直线AD1和DC1所成角,由此利用氽弦定理能求出异面直线AD1和DC1所成角的余弦值.
解答:
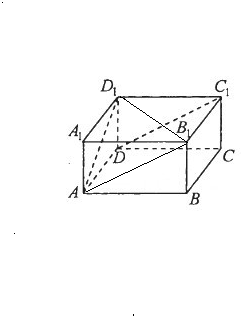 解:连结AB1,D1B1,
解:连结AB1,D1B1,
∵AB1∥DC1,
∴∠D1AB1是异面直线AD1和DC1所成角,
在长方体ABCD-A1B1C1D1中,
∵底面是边长为2的正方形,高为1,
∴AB1=
,AD1=
,D1B1=2
,
∴cos∠D1AB1=
=
.
∴异面直线AD1和DC1所成角的余弦值
.
故选:B.
 解:连结AB1,D1B1,
解:连结AB1,D1B1,∵AB1∥DC1,
∴∠D1AB1是异面直线AD1和DC1所成角,
在长方体ABCD-A1B1C1D1中,
∵底面是边长为2的正方形,高为1,
∴AB1=
| 5 |
| 5 |
| 2 |
∴cos∠D1AB1=
(
| ||||||
2×
|
| 1 |
| 5 |
∴异面直线AD1和DC1所成角的余弦值
| 1 |
| 5 |
故选:B.
点评:本题考查异面直线所面角的余弦值的求法,是基础题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题P:?x∈(0,1),x2<x3;命题q:若函数f(x)=ln(a+
)为奇函数,则a=-1,下列命题中真命题是( )
| 2 |
| x+1 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∧¬q |
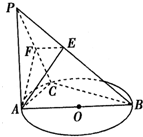 如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC,
正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离小于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知双曲线
-
=1(a>0,b>0)左,右焦点分别为F1、F2.若在双曲线右支上存在一点P使|PF1|=4|PF2|,则双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
| B、(1,2] | ||
C、[
| ||
D、[
|
已知函数f(x)=
,若方程f(x)=ax恰有两个不同的实根时,则实数a的取值范围是( )
|
| A、(0,e) | ||
B、(
| ||
| C、(e,4] | ||
| D、(0,4) |
已知数列{an}的通项an=2ncos(nπ),则a1+a2+…+a99+a100=( )
| A、0 | ||
B、
| ||
| C、2-2101 | ||
D、
|
设向量
=(cosα,sinα),
=(sinβ,cosβ),若
•
=-
,则<
,
>=( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、-30° |
| C、150° | D、120° |