题目内容
双曲线
-
=1的渐近线方程是( )
| y2 |
| 9 |
| x2 |
| 16 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线渐近线方程的公式加以计算,可得答案.
解答:
解:双曲线
-
=1中a=3且b=4,双曲线的渐近线方程为y=±
x,即y=±
x.
故选:A.
| y2 |
| 9 |
| x2 |
| 16 |
| a |
| b |
| 3 |
| 4 |
故选:A.
点评:本题给出双曲线的方程,求它的渐近线.着重考查了双曲线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
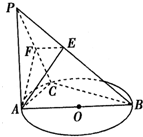 如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:
如图,PA垂直于圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影,给出下列结论:①AF⊥PB②EF⊥PB③AF⊥BC④AE⊥BC,
正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
已知数列{an}的通项an=2ncos(nπ),则a1+a2+…+a99+a100=( )
| A、0 | ||
B、
| ||
| C、2-2101 | ||
D、
|
设向量
=(cosα,sinα),
=(sinβ,cosβ),若
•
=-
,则<
,
>=( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、30° | B、-30° |
| C、150° | D、120° |
已知空间四边形OABC各边及对角线长都相等,E,F分别为AB,OC的中点,则异面直线OE与BF所成角的余弦值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
复数z=
的共轭复数在复平面内对应的点在( )
| 1+2i2015 |
| 1-i2015 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在△ABC中,AC=
,BC=2,B=60°,则AB等于( )
| 7 |
| A、4 | B、3 | C、2 | D、1 |
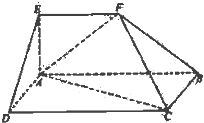 在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.