题目内容
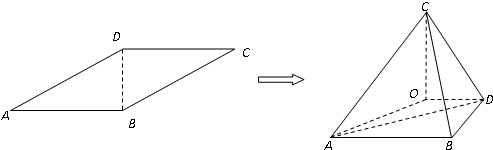
如图,平行四边形ABCD中,AB⊥BD,AB=2,BD=
,沿BD将△BCD折起,使二面角A-BD-C是大小为锐角α的二面角,设C在平面ABD上的射影为O.
(1)求证:OD∥AB;
(2)当α为何值时,三棱锥C-OAD的体积最大?最大值为多少?
| 2 |
(1)求证:OD∥AB;
(2)当α为何值时,三棱锥C-OAD的体积最大?最大值为多少?

考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:(1)首先,得到BD⊥平面SCD,然后,得到BD⊥OD,从而得证;
(2)根据射影,得到BD⊥OD,然后,根据体积公式,得到VC-AOD=
S△AOD•OC,从而求解体积.
(2)根据射影,得到BD⊥OD,然后,根据体积公式,得到VC-AOD=
| 1 |
| 3 |
解答:
解:(1)∵CO⊥平面ABD,
CO⊥BD,
∵BD⊥CD,CD∩CO=C,
∴BD⊥平面OCD
又OD?平面COD,
∴BD⊥OD,
∵AB⊥BD,
∴AB∥OD.
(2)由题知OD为CD在平面ABD上的射影,
∵BD⊥CD,CO⊥平面ABD,
∴BD⊥OD,
∴∠ODC=α,
VC-AOD=
S△AOD•OC=
•
•OD•BD•OC=
•OD•OC
=
•CD•sinα•CD•cosα
=
sin2α≤
,
当且仅当sin2α=1,即α=45°时取等号,
∴当α=45°时,三棱锥O-ACD的体积最大,最大值为
.

CO⊥BD,
∵BD⊥CD,CD∩CO=C,
∴BD⊥平面OCD
又OD?平面COD,
∴BD⊥OD,
∵AB⊥BD,
∴AB∥OD.
(2)由题知OD为CD在平面ABD上的射影,
∵BD⊥CD,CO⊥平面ABD,
∴BD⊥OD,
∴∠ODC=α,
VC-AOD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
=
| ||
| 6 |
=
| ||
| 3 |
| ||
| 3 |
当且仅当sin2α=1,即α=45°时取等号,
∴当α=45°时,三棱锥O-ACD的体积最大,最大值为
| ||
| 3 |

点评:本题重点考查了空间中垂直关系、平行关系及其判断方法、投影的概念、空间中关于角度的认识等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}的通项an=2ncos(nπ),则a1+a2+…+a99+a100=( )
| A、0 | ||
B、
| ||
| C、2-2101 | ||
D、
|
在△ABC中,AC=
,BC=2,B=60°,则AB等于( )
| 7 |
| A、4 | B、3 | C、2 | D、1 |
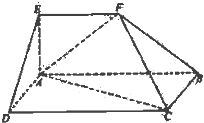 在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.