题目内容
将一个边长为10的大正方体的表面涂成红色后，再切成边长为1的小正方形，这些小正方形中至少有一面涂成红色的个数是 ．
考点：棱柱的结构特征
专题：计算题,排列组合
分析：至少有一面涂成红色，可分为三类：①只有一面涂色，有6×（10-2）2=384个，②有两面涂色，有8×12=96个，③有三面涂色的，有8个．再由计数原理，即可得到．
解答：
解：对照正方体，这些小正方体中至少有一面涂成红色，可分为：
①只有一面涂色，有6×（10-2）2=384个，
②有两面涂色，有8×12=96个，
③有三面涂色的，有8个．
则共有384+96+8=488个．
故答案为：488．
①只有一面涂色，有6×（10-2）2=384个，
②有两面涂色，有8×12=96个，
③有三面涂色的，有8个．
则共有384+96+8=488个．
故答案为：488．
点评：本题考查正方体的特征，考查分类相加原理，考查运算能力，属于基础题．
练习册系列答案
中考解读考点精练系列答案
相关题目
下列各组函数中，表示同一函数的是（ ）
A、y=1，y=
| ||||||
B、y=
| ||||||
| C、y=2x+1-2x，y=2x | ||||||
| D、y=2lgx，y=lgx2 |
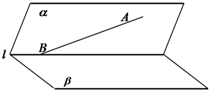如图，已知二面角α-l-β的大小是60°，线段AB∈α．B∈l，AB与l所成的角为30°，则AB与平面β所成的角的正弦值是已知函数f（x）=
，若a＞0，b＞0，c＞0，a+b＞c，则（ ）
| x |
| x+1 |
| A、f（a）+f（b）＞f（c） |
| B、f（a）+f（b）=f（c） |
| C、f（a）+f（b）＜f（c） |
| D、以上结论都不对 |
