题目内容
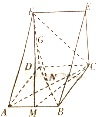 已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.
已知直三棱柱BCE-ADG,底面△ADF中,AD⊥DF,DA=DF=DC,其中M,N分别是AB,AC的中点,G是DF上的一个动点.(1)求证:GN⊥AC;
(2)当DC=
| 1 |
| 3 |
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)要证GN⊥AC,只要证明AC垂直于平面FDN即可,由DF垂直于底面,底面是正方形即可得到答案;
(2)由DC=
DF时,在边AD上存在一点P,使得GP∥平面FMC,此时P为AD的中点.在根据线面平行、面面平行去证即可.
(2)由DC=
| 1 |
| 3 |
解答:
解:(1)AD⊥DF,DF=AD=DC,
连接DB,可知B、N、D共线,且AC⊥DN,
又FD⊥AD,FD⊥CD,且AD∩CD=D.
所以FD⊥平面ABCD,所以AC⊥平面FDN.
GN?平面FDN,
∴GN⊥AC.
(2)当DC=
DF时,在边AD上存在一点P,使得GP∥平面FMC,此时P为AD的中点.
证明如下:在DC上取点S,使DS=
DC.连接GS.
因为DG=
DF,DS=
DC,
所以GS∥FC,
∴GS∥平面FMC,
延长BA至点Q,使得AQ=
AM.连接SQ交AD与点P,
可得PS∥CM,
∴PS∥平面EMC,
由GS∩PS=S,
∴PS∥平面EMC,
由GS∩PS=S,
∴平面GSP∥平面EMC,
又GP?平面GSP,
∴GP∥平面FMC
连接DB,可知B、N、D共线,且AC⊥DN,
又FD⊥AD,FD⊥CD,且AD∩CD=D.
所以FD⊥平面ABCD,所以AC⊥平面FDN.
GN?平面FDN,
∴GN⊥AC.
(2)当DC=
| 1 |
| 3 |
证明如下:在DC上取点S,使DS=
| 1 |
| 3 |
因为DG=
| 1 |
| 3 |
| 1 |
| 3 |
所以GS∥FC,
∴GS∥平面FMC,
延长BA至点Q,使得AQ=
| 1 |
| 3 |
可得PS∥CM,
∴PS∥平面EMC,
由GS∩PS=S,
∴PS∥平面EMC,
由GS∩PS=S,
∴平面GSP∥平面EMC,
又GP?平面GSP,
∴GP∥平面FMC
点评:本题考查了直线与平面平行的判定,考查了直线与平面垂直的性质,综合考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列各组函数中,表示同一函数的是( )
A、y=1,y=
| ||||||
B、y=
| ||||||
| C、y=2x+1-2x,y=2x | ||||||
| D、y=2lgx,y=lgx2 |
集合{a,b}的子集个数为( )
| A、4 | B、3 | C、2 | D、1 |
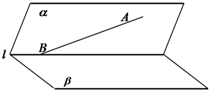 如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是