题目内容
设函数f(x)的定义域为集合A,值域为集合B,若函数满足A⊆B,则称函数为“集中函数“,已知函数f(x)=
为“集中函数“,则实数a的取值范围是 .
| ax2+2x |
考点:函数的值域,集合的包含关系判断及应用
专题:计算题,函数的性质及应用
分析:讨论a的取值,从而求出集合A、B,由A⊆B解a.
解答:
解:①若a=0,则A=[0,+∞),B=[0,+∞),成立;
②若a>0,则A=(-∞,-
]∪[0,+∞),B=[0,+∞),不成立;
③若a<0,则A=[0,-
],B=[0,-
],
则由A⊆B知,-
≤-
,无解,
综上所述,a=0.
故答案为:a=0.
②若a>0,则A=(-∞,-
| 2 |
| a |
③若a<0,则A=[0,-
| 2 |
| a |
| 1 |
| a |
则由A⊆B知,-
| 2 |
| a |
| 1 |
| a |
综上所述,a=0.
故答案为:a=0.
点评:本题考查了函数的定义域与值域的求法,同时考查了分类讨论的数学思想,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知x>0时,(x-1)f′(x)<0,若△ABC是锐角三角形,则一定成立的是( )
| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)>f(cosB) |
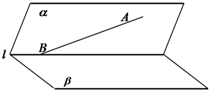 如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是