题目内容
设a∈Z，实数x，y满足约束条件
，若点（x，y）构成的平面区域中恰好含2个整点（横、纵坐均匀整数），则2x-y的最大值是（ ）
|
| A、-2 | B、-1 | C、0 | D、2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用条件求出a的值，利用数形结合即可得到结论．
解答：
解：作出不等式组对应的平面区域如图：若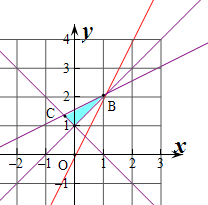
点（x，y）构成的平面区域中恰好含2个整点（横、纵坐均匀整数），
则可行域内的两个整点分别为（0，1），（1，2），
∵a是整数，
∴直线x-2y+a=0必过点B（1，2），此时a=3，
由z=2x-y得y=-2x-z，
平移直线y=-2x-z，
当直线y=-2x-z经过点B（1，2）时，z取得最大值，
为z=2-2=0，
故选：C
点（x，y）构成的平面区域中恰好含2个整点（横、纵坐均匀整数），则可行域内的两个整点分别为（0，1），（1，2），
∵a是整数，
∴直线x-2y+a=0必过点B（1，2），此时a=3，
由z=2x-y得y=-2x-z，
平移直线y=-2x-z，
当直线y=-2x-z经过点B（1，2）时，z取得最大值，
为z=2-2=0，
故选：C
点评：本题主要考查线性规划的应用，根据条件求出a的值是解决本题的关键，利用数形结合是解决此类问题的基本方法．
练习册系列答案
阅读快车系列答案
相关题目
已知i是虚数单位，则复数（
）2的虚部是（ ）
| 3i | ||
|
| A、1 | ||
| B、-1 | ||
C、-2
| ||
D、2
|
函数f（x）=2x+1和函数g（x）=log2（x+3）的图象的交点一定在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
命题p：若a，b∈R，则|a|+|b|＞1是|a+b|＞1的充分不必要条件；命题q：函数y=
的定义域是（-∞，1]，则（ ）
log
|
| A、“p或q”为假 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p假q真 |