题目内容
命题p:若a,b∈R,则|a|+|b|>1是|a+b|>1的充分不必要条件;命题q:函数y=
的定义域是(-∞,1],则( )
log
|
| A、“p或q”为假 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p假q真 |
考点:复合命题的真假
专题:简易逻辑
分析:根据复合命题之间的关系,先判定命题p,q的真假,即可得到结论.
解答:
解:由绝对值不等式的性质可知,|a|+|b|>|a+b|,
∴当a=2,b=-2时,满足|a|+|b|>1但|a+b|>1不成立,即充分性不成立,
若|a+b|>1,则|a|+|b|>1成立,即|a|+|b|>1是|a+b|>1的必要不充分条件,即命题p为假命题.
要使函数有意义,则log
(3x-2)≥0,即0<3x-2≤1,即
<x≤1,即函数的定义域为(
,1],故命题q为假命题,
则“p或q”为假,
故选:A
∴当a=2,b=-2时,满足|a|+|b|>1但|a+b|>1不成立,即充分性不成立,
若|a+b|>1,则|a|+|b|>1成立,即|a|+|b|>1是|a+b|>1的必要不充分条件,即命题p为假命题.
要使函数有意义,则log
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
则“p或q”为假,
故选:A
点评:本题主要考查复合命题真假之间的关系,比较基础.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知f(x)=
x3+ax2+x是奇函数,则f(3)+f′(1)=( )
| 1 |
| 3 |
| A、14 | B、12 | C、10 | D、-8 |
执行如图所示的程序框图,输出的S值为( )


| A、2 | B、-2 | C、4 | D、-4 |
设a∈Z,实数x,y满足约束条件
,若点(x,y)构成的平面区域中恰好含2个整点(横、纵坐均匀整数),则2x-y的最大值是( )
|
| A、-2 | B、-1 | C、0 | D、2 |
已知i是虚数单位,若(2i-1)z=5,则复数z在复平面内对应的点的坐标为( )
| A、(-2,-1) |
| B、(2,-1) |
| C、(-1,-2) |
| D、(-1,2) |
已知x,y满足不等式组
,则
的取值范围是( )
|
| 2y+x |
| x |
| A、[1,4] |
| B、[2e+1,9] |
| C、[3,2e+1] |
| D、[1,e] |

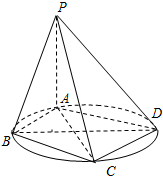 (理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=
(理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=