题目内容
设双曲线C:
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,点M在双曲线C上,且|MF1|-|MF2|=2
,已知双曲线C的离心率为
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)过双曲线C上一动点P向圆E:x2+(y-4)2=1作两条切线,切点分别为A,B,求
•
的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
(Ⅰ)求双曲线C的方程;
(Ⅱ)过双曲线C上一动点P向圆E:x2+(y-4)2=1作两条切线,切点分别为A,B,求
| PA |
| PB |
考点:双曲线的标准方程,向量在几何中的应用
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)根据题设条件由双曲线定义知a=
,e=
=
,由此能求出双曲线C的方程.
(Ⅱ)连AE,由题意知AE⊥AP,且|AE|=1.设|PE|=t,∠APB=2θ,则|PA|=|PB|=
,sinθ=
=
,由此利用导数性质和圆的知识能求出
•
的最小值.
| 2 |
| c |
| a |
| 2 |
(Ⅱ)连AE,由题意知AE⊥AP,且|AE|=1.设|PE|=t,∠APB=2θ,则|PA|=|PB|=
| t2-1 |
| |AE| |
| |PE| |
| 1 |
| t |
| PA |
| PB |
解答:
解:(Ⅰ)∵双曲线C:
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,
点M在双曲线C上,且|MF1|-|MF2|=2
,
∴由双曲线定义知:a=
,
∵双曲线C的离心率为
,∴e=
=
,
解得c=2,∴b2=22-(
)2=2,
∴双曲线C的方程是
-
=1.…(4分)
(Ⅱ)连AE,则AE⊥AP,且|AE|=1.
设|PE|=t,∠APB=2θ,
则|PA|=|PB|=
,sinθ=
=
.…(6分)
∴
•
=|
|•|
|cos2θ
=(t2-1)(1-2sin 2 θ)
=(t2-1)(1-
)
=t2+
-3.…(8分)
设点P(x,y),则x2-y2=2.又圆心E(0,4),
则t2=|PE|2=x2+(y-4)2
=(y2+2)+(y-4)2
=2y2-8y+18
=2(y-2)2+10≥10,…(10分)
设f(t)=t2+
-3,则当t≥
时,f′(t)=2t-
=
>0,
∴f(t)在[
,+∞)上是增函数,
∴f(t)min=f(
)=
,
∴
•
的最小值为
.…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
点M在双曲线C上,且|MF1|-|MF2|=2
| 2 |
∴由双曲线定义知:a=
| 2 |
∵双曲线C的离心率为
| 2 |
| c |
| a |
| 2 |
解得c=2,∴b2=22-(
| 2 |
∴双曲线C的方程是
| x2 |
| 2 |
| y2 |
| 2 |
(Ⅱ)连AE,则AE⊥AP,且|AE|=1.
设|PE|=t,∠APB=2θ,
则|PA|=|PB|=
| t2-1 |
| |AE| |
| |PE| |
| 1 |
| t |
∴
| PA |
| PB |
| PA |
| PB |
=(t2-1)(1-2sin 2 θ)
=(t2-1)(1-
| 2 |
| t2 |
=t2+
| 2 |
| t2 |
设点P(x,y),则x2-y2=2.又圆心E(0,4),
则t2=|PE|2=x2+(y-4)2
=(y2+2)+(y-4)2
=2y2-8y+18
=2(y-2)2+10≥10,…(10分)
设f(t)=t2+
| 2 |
| t2 |
| 10 |
| 4 |
| t3 |
| 2(t4-2) |
| t3 |
∴f(t)在[
| 10 |
∴f(t)min=f(
| 10 |
| 36 |
| 5 |
∴
| PA |
| PB |
| 36 |
| 5 |
点评:本题考查双曲线方程和数量积最小值的求法,是中档题,解题时要认真审题,注意双曲线的定义和导数性质的灵活运用.

练习册系列答案
相关题目
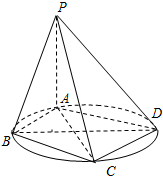 (理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=
(理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=