题目内容
已知函数f(x)在R上是增函数,g(x)在R上是减函数.求证:函数F(x)=f(x)-g(x)在R上是增函数.
考点:函数单调性的性质
专题:函数的性质及应用
分析:任取x1,x2∈R,且x1<x2,则由于f(x)在R上是增函数,g(x)在R上是减函数,有f(x1)<f(x2),g(x1)>g(x2),
从而F(x1)-F(x2)<0,进而F(x1)<F(x2).
从而F(x1)-F(x2)<0,进而F(x1)<F(x2).
解答:
解:任取x1,x2∈R,且x1<x2,
则由于f(x)在R上是增函数,g(x)在R上是减函数,
有f(x1)<f(x2),g(x1)>g(x2),
∴F(x1)-F(x2)=[f(x1)-g(x1)]-[f(x2)-g(x2)]
=[f(x1)-f(x2)]-[g(x1)-g(x2)]
<0,
∴F(x1)<F(x2)
∴函数F(x)在R上是增函数.
则由于f(x)在R上是增函数,g(x)在R上是减函数,
有f(x1)<f(x2),g(x1)>g(x2),
∴F(x1)-F(x2)=[f(x1)-g(x1)]-[f(x2)-g(x2)]
=[f(x1)-f(x2)]-[g(x1)-g(x2)]
<0,
∴F(x1)<F(x2)
∴函数F(x)在R上是增函数.
点评:本题考察了函数的单调性,函数的单调性的证明,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若角α的终边在直线y=-2x上,且sina>0,则cosa值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
| D、-2 |
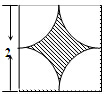 如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
(
-
)n的展开式中只有第5项的二项式系数最大,则展开式中的常数项是( )
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |
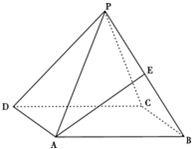 正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.
正四棱锥P-ABCD中,侧面与底面ABCD所成的角为60°,E是PB的中点,求异面直线PD与AE所成角的大小.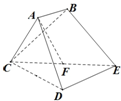 已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.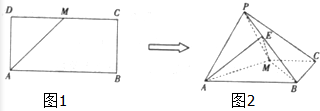 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=