题目内容
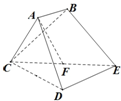 已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.(Ⅰ)求证:AF⊥CD
(Ⅱ)求直线AC与平面CBE所成角的余弦值.
考点:点、线、面间的距离计算,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(I)取CD的中点O,连接AG,GF,则GF∥DE,证明CD⊥平面AGF,由线面垂直的性质,我们可以得到AF⊥CD;
(II)分别以
,
,
为x,y,z轴建立空间坐标系,求出各个顶点的坐标,进而求出平面CBE的法向量,代入向量夹角公式,即可得到直线AC与平面CBE所成角的余弦值.
(II)分别以
| GD |
| GF |
| GA |
解答:
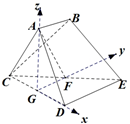 (Ⅰ)证明:取CD的中点,连接AG,GF,则GF∥DE.
(Ⅰ)证明:取CD的中点,连接AG,GF,则GF∥DE.
∵AC=AD,∴AG⊥CD,
∵DE⊥平面ACD,∴DE⊥CD,∴GF⊥CD.
∵AG∩GF=G,∴CD⊥平面AGF.
∵AF?平面AGF,
∴CD⊥AF;
(Ⅱ)解:分别以
,
,
为x,y,z轴,建立如图所示的空间直角坐标系G-xyz.
则A(0,0,
),B(0,1,
),C(-1,0,0),E(1,2,0),
∴
=(1,1,
),
=(2,2,0),
=(1,0,
).
设平面CBE的法向量为
=(x,y,z),
则
设x=1,则
=(1,-1,0),
∴cos<
,
>=
=
设直线AC与平面CBE所成角为θ,则sinθ=cos<
,
>=
=
,
∴cosθ=
=
,
∴直线AC与平面CBE所成角的余弦值为
.
 (Ⅰ)证明:取CD的中点,连接AG,GF,则GF∥DE.
(Ⅰ)证明:取CD的中点,连接AG,GF,则GF∥DE.∵AC=AD,∴AG⊥CD,
∵DE⊥平面ACD,∴DE⊥CD,∴GF⊥CD.
∵AG∩GF=G,∴CD⊥平面AGF.
∵AF?平面AGF,
∴CD⊥AF;
(Ⅱ)解:分别以
| GD |
| GF |
| GA |
则A(0,0,
| 3 |
| 3 |
∴
| CB |
| 3 |
| CE |
| CA |
| 3 |
设平面CBE的法向量为
| n |
则
|
设x=1,则
| n |
∴cos<
| CA |
| n |
| ||||
|
|
| ||
| 4 |
设直线AC与平面CBE所成角为θ,则sinθ=cos<
| CA |
| n |
| ||||
|
|
| ||
| 4 |
∴cosθ=
1-(
|
| ||
| 4 |
∴直线AC与平面CBE所成角的余弦值为
| ||
| 4 |
点评:本题考查的知识点是直线与平面垂直的性质及直线与平面所成角的求法,在使用向量法求直线与平面所成角的大小时,建立坐标系,求出平面的法向量是关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
复数(
+
i)3(i为虚数单位)的值是( )
| 1 |
| 2 |
| ||
| 2 |
| A、-1 | B、1 | C、-i | D、i |
函数f(x)=
的定义域为 ( )
| lg(x+1) |
| x-2 |
| A、(-1,+∞) |
| B、(-∞,2)∪(2,+∞) |
| C、(-1,2)∪(2,+∞) |
| D、(2,+∞) |
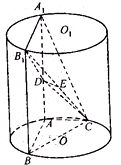 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.