Question

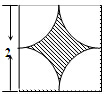如图所示，墙上挂有边长为2的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为1的圆孤，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则它击中阴影部分的概率是（　　）

• A、

  π

  4

• B、

  π

  8

• C、1-

  π

  4

• D、1-

  π

  8

Answer 1

考点：几何概型

专题：计算题,概率与统计

分析：欲求击中阴影部分的概率，则可先求出正方形的面积，再求阴影部分区域的面积，进而根据几何概型概率公式易求解．

解答： 解：根据题意，图中正方形的面积为2×2=4，
图中阴影部分的面积为：4-4×

1

4

×π×1²=4-π，
则它击中阴影部分的概率P=

4-π

4

=1-

π

4

故选：C．

点评：本题考查几何概型的计算，注意正确计算出的各个面积，进而由几何概型公式计算即可．