题目内容
某市为考核一学校的教学质量,对该校甲、乙两班各50人进行测验,根据这两班的成绩绘制茎叶图如图所示:

(1)求甲、乙两班成绩的中位数,并将甲乙两班数据合在一起,绘出这些数据的频率分布直方图;
(2)根据抽样测验,能否认为该学校“教学成绩不低于70分的学生至少占全体学生的80%”?
(3)根据茎叶图,分析甲、乙两班成绩的特点.

(1)求甲、乙两班成绩的中位数,并将甲乙两班数据合在一起,绘出这些数据的频率分布直方图;
(2)根据抽样测验,能否认为该学校“教学成绩不低于70分的学生至少占全体学生的80%”?
(3)根据茎叶图,分析甲、乙两班成绩的特点.
考点:频率分布直方图,茎叶图
专题:概率与统计
分析:(1)根据中位数的定义,求出甲、乙两班的中位数,求出每一小组的频率,画出频率分布直方图;
(2)计算教学成绩不低于70分的学生占全体学生的比例数值是多少,得出统计结论;
(3)根据甲、乙两班成绩的中位数与数据的集中情况,分析甲、乙两班的成绩特点.
(2)计算教学成绩不低于70分的学生占全体学生的比例数值是多少,得出统计结论;
(3)根据甲、乙两班成绩的中位数与数据的集中情况,分析甲、乙两班的成绩特点.
解答:
解:(1)甲班50名学生成绩从小到大排列,排在第25、26位的是72和73,
所以甲班成绩的中位数是
=72.5;
乙班50名学生成绩从小到大排列,排在第25、26位的是78和78,
所以乙班成绩的中位数是
=78;
[50,60)以上的频数为5,[60,70)以上的频数为20,
[70,80)以上的频数为45,[80,90)以上的频数为25,
[90,100]以上的频数为5,画出频率分布直方图,如图所示;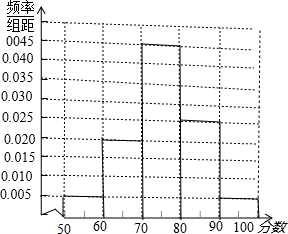
(2)教学成绩不低于70分的学生至少占全体学生的比例的估计值为
=10(0.045+0.025+0.005)=0.75,
0.75<0.8,
所以不能认为该校符合“教学成绩不低于70分的学生至少占全体学生的80%”的规定;
(3)甲班成绩中位数低于乙班,且从茎叶图可以大致看出,甲班的标准差小于乙班;
说明甲班成绩低于乙班,但全班学生成绩较为集中,乙班成绩高于甲班,但学生间的差异性较大.
所以甲班成绩的中位数是
| 72+73 |
| 2 |
乙班50名学生成绩从小到大排列,排在第25、26位的是78和78,
所以乙班成绩的中位数是
| 78+78 |
| 2 |
[50,60)以上的频数为5,[60,70)以上的频数为20,
[70,80)以上的频数为45,[80,90)以上的频数为25,
[90,100]以上的频数为5,画出频率分布直方图,如图所示;

(2)教学成绩不低于70分的学生至少占全体学生的比例的估计值为
| 45+25+5 |
| 100 |
0.75<0.8,
所以不能认为该校符合“教学成绩不低于70分的学生至少占全体学生的80%”的规定;
(3)甲班成绩中位数低于乙班,且从茎叶图可以大致看出,甲班的标准差小于乙班;
说明甲班成绩低于乙班,但全班学生成绩较为集中,乙班成绩高于甲班,但学生间的差异性较大.
点评:本题考查了频率分布直方图的应用问题,也考查了中位数与方差的应用问题,是基础题目.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
不等式组
表示的平面区域的面积等于 ( )
|
A、
| ||
| B、6 | ||
| C、9 | ||
| D、18 |
已知函数f(x)=2x+2x-6,用二分法求方程2x+2x-6=0在x∈(1,3)内近似解的过程中,取区间中点x0=2,那么下一个有根区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(2,2.5) |
| D、(2.5,3) |
下列函数中,在(0,+∞)上为减函数的是( )
| A、y=log2(x+1) | ||
B、y=-
| ||
C、y=
| ||
D、y=(
|
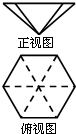 已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为
已知一个底面为正六边形,侧棱长都相等的六棱锥的正视图与俯视图如图所示,若该几何体的底面边长为2,侧棱长为