题目内容
对于给定的大于1的正整数n,设x=a0+a1n+a2n2+…+annn,其中ai∈{0,1,2,…,n-1},i=1,2,…,n-1,n,且an≠0,记满足条件的所有x的和为An.
(1)求A2
(2)设An=
•f(n),求f(n)
(1)求A2
(2)设An=
| nn(n-1) |
| 2 |
考点:计数原理的应用
专题:等差数列与等比数列,点列、递归数列与数学归纳法,排列组合
分析:(1)当n=2时,x=a0+2a1+4a2,a0∈{0,1},a1∈{0,1},a2=1,故满足条件的x共有4个,求出它们的和即可;
(2)由分步计数原理求出满足条件的x共有nn(n-1)个,求出An中所有含an项的和,化简即可
(2)由分步计数原理求出满足条件的x共有nn(n-1)个,求出An中所有含an项的和,化简即可
解答:
解:(1)当n=2时,x=a0+2a1+4a2,a0∈{0,1},a1∈{0,1},a2=1,
故满足条件的x共有4个,
分别为:x=0+0+4,x=0+2+4,x=1+0+4,x=1+2+4,
它们的和是22.
(2)由题意得,a0,a1,a2,…,an-1各有n种取法;an有n-1种取法,
由分步计数原理可得a0,a1,a2,…,an-1的不同取法共有n•n•…n•(n-1)=nn(n-1),
即满足条件的x共有nn(n-1)个,
当a0分别取0,1,2,…,n-1时,a1,a2,…,an-1各有n种取法,an有n-1种取法,
故An中所有含a0项的和为(0+1+2+…+n-1)nn-1(n-1)=
;
同理,An中所有含a1项的和为(0+1+2+…+n-1)nn-1(n-1)•n=
•n;
An中所有含a2项的和为(0+1+2+…+n-1)nn-1(n-1)•n2=
•n2;
An中所有含an-1项的和为(0+1+2+…+n-1)nn-1(n-1)•nn-1=
•nn-1;
当an分别取i=1,2,…,n-1时,a0,a1,a2,…,an-1各有n种取法,
故An中所有含an项的和为(1+2+…+n-1)nn•nn=
•nn;
所以An=
(1+n+n2+…+nn-1)+
•nn=
+
•nn=
(nn+1+nn-1)
故f(n)=(nn+1+nn-1)
故满足条件的x共有4个,
分别为:x=0+0+4,x=0+2+4,x=1+0+4,x=1+2+4,
它们的和是22.
(2)由题意得,a0,a1,a2,…,an-1各有n种取法;an有n-1种取法,
由分步计数原理可得a0,a1,a2,…,an-1的不同取法共有n•n•…n•(n-1)=nn(n-1),
即满足条件的x共有nn(n-1)个,
当a0分别取0,1,2,…,n-1时,a1,a2,…,an-1各有n种取法,an有n-1种取法,
故An中所有含a0项的和为(0+1+2+…+n-1)nn-1(n-1)=
| nn(n-1)2 |
| 2 |
同理,An中所有含a1项的和为(0+1+2+…+n-1)nn-1(n-1)•n=
| nn(n-1)2 |
| 2 |
An中所有含a2项的和为(0+1+2+…+n-1)nn-1(n-1)•n2=
| nn(n-1)2 |
| 2 |
An中所有含an-1项的和为(0+1+2+…+n-1)nn-1(n-1)•nn-1=
| nn(n-1)2 |
| 2 |
当an分别取i=1,2,…,n-1时,a0,a1,a2,…,an-1各有n种取法,
故An中所有含an项的和为(1+2+…+n-1)nn•nn=
| nn+1(n-1) |
| 2 |
所以An=
| nn(n-1)2 |
| 2 |
| nn+1(n-1) |
| 2 |
| nn(n-1)2 |
| 2 |
| nn-1 |
| n-1 |
| nn+1(n-1) |
| 2 |
| nn(n-1) |
| 2 |
故f(n)=(nn+1+nn-1)
点评:本题考查了分步计数原理,以及等比数列的问题,培养了学生的转化能力,知识的应用能力,属于难题

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
图中所示的四个图形中正确的是( )
A、 |
B、 |
C、 |
D、 |
若某几何体的三视图如图所示,则这个几何体的体积为( )
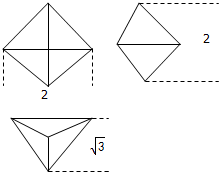

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
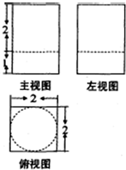 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A、12+π | B、6+π |
| C、12-π | D、6-π |
