题目内容
已知a,b为两个正数,且a>b,设a1=
,b1=
,当n≥2,n∈N*时,an=
,bn=
.
(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
(an-bn);
(Ⅲ)设数列{an},{bn}前n项和分别为SnTn,求证:Sn<Tn+2(a+b).
| a+b |
| 2 |
| ab |
| an-1+bn-1 |
| 2 |
| an-1bn-1 |
(Ⅰ)求证:数列{an}是递减数列,数列{bn}是递增数列;
(Ⅱ)求证:an+1-bn+1<
| 1 |
| 2 |
(Ⅲ)设数列{an},{bn}前n项和分别为SnTn,求证:Sn<Tn+2(a+b).
考点:数列与不等式的综合,数列的函数特性,数列的求和
专题:证明题
分析:(I)易知对任意n∈N*,an>0,bn>0.根据基本不等式可知对任意n∈N*,an>bn,an+1-an=
-an判定符号可得数列{an}的单调性,bn+1-bn=
-bn=
(
-
)>0,从而得到数列{bn}的单调性;
(II)根据题意可知an+1-bn+1=
-
,然后利用放缩法即可证得结论;
(III)根据(II)可得an-bn<(a-b)•(
)n-1,从而
,最后利用放缩法即可证得结论.
| an+bn |
| 2 |
| anbn |
| bn |
| an |
| bn |
(II)根据题意可知an+1-bn+1=
| an+bn |
| 2 |
| anbn |
(III)根据(II)可得an-bn<(a-b)•(
| 1 |
| 2 |
|
解答:
(Ⅰ)证明:易知对任意n∈N*,an>0,bn>0.
由a≠b,可知
>
,即a1>b1.
同理,
>
,即a2>b2.
可知对任意n∈N*,an>bn.an+1-an=
-an=
<0,
所以数列{an}是递减数列.bn+1-bn=
-bn=
(
-
)>0,
所以数列{bn}是递增数列. …(5分)
(Ⅱ)证明:an+1-bn+1=
-
<
-
<
(an-bn).…(10分)
(Ⅲ)解:由an+1-bn+1<
(an-bn),可得an-bn<(a-b)•(
)n-1.
∴Sn<Tn+2(a+b).…(14分)
由a≠b,可知
| a+b |
| 2 |
| ab |
同理,
| a1+b1 |
| 2 |
| a1b1 |
可知对任意n∈N*,an>bn.an+1-an=
| an+bn |
| 2 |
| bn-an |
| 2 |
所以数列{an}是递减数列.bn+1-bn=
| anbn |
| bn |
| an |
| bn |
所以数列{bn}是递增数列. …(5分)
(Ⅱ)证明:an+1-bn+1=
| an+bn |
| 2 |
| anbn |
| an+bn |
| 2 |
| bnbn |
| 1 |
| 2 |
(Ⅲ)解:由an+1-bn+1<
| 1 |
| 2 |
| 1 |
| 2 |
|
∴Sn<Tn+2(a+b).…(14分)
点评:本题主要考查了数列的单调性的判定,以及利用放缩法证明不等式,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目
抛物线y2=2px(p>0)的焦点到双曲线
-
=1渐近线的距离为
,则实数p等于( )
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
| A、2 | B、4 | C、8 | D、16 |
在极坐标系中,圆ρ=2cosθ的圆心到直线ρcos(θ-
)=1的距离是( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
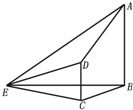 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.