题目内容
已知焦点为F1(-1,0),F2(1,0)的椭圆经过点(1,
),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求
•
的范围;
(Ⅲ)若直线AB的斜率存在且不为零,向量
+
与向量
=(-2
,1)平行,求
•
的值及△AOB的外接圆的方程.
| ||
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)求
| OA |
| OB |
(Ⅲ)若直线AB的斜率存在且不为零,向量
| OA |
| OB |
| a |
| 2 |
| OA |
| OB |
考点:圆与圆锥曲线的综合,向量在几何中的应用,椭圆的标准方程
专题:计算题,转化思想
分析:(1)直接把椭圆经过点(1,
)的坐标代入方程,再结合焦点坐标即可求椭圆的方程;
(2)把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,再代入
•
的表达式即可求出求
•
的范围;
(3)先把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,求出
+
,利用
+
与向量
=(-2
,1)共线求出直线斜率进而求出求
•
的值及△AOB的外接圆方程.
| ||
| 2 |
(2)把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,再代入
| OA |
| OB |
| OA |
| OB |
(3)先把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,求出
| OA |
| OB |
| OA |
| OB |
| a |
| 2 |
| OA |
| OB |
解答:
解:(1)设椭圆方程为
+
=1(a>b>0).
由题得
=1⇒a2=2,b2=1,
所以椭圆的方程是
+y2=1,
(2)当K存在时,设直线方程为y=K(x-1).
联立
,化简为(2k2+1)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2)x1+ x2=
,x1•x2=
.
•
=x1x2+y1y2=x1x2+k2(x1-1) (x2-1)
∴
•
=
(#)
令
=m则k2=
≥0
∴-2≤m<
,∴-2≤
•
<
当K不存在时,A(1,
),B(1,-
),则
•
=
综上,-2≤
•
≤
.
(3)
•
=(x1+x2,y1+y2)
∴-2
(y1+y2)=x1+x2,
∴-2
(k(x1-1)+k(x2-1))=x1+x2
由韦达定理知k=0或k=
代入(#)得
•
=-2或0
当
•
=-2时,A,O,B共线,不存在外接圆
当
•
=0时,
⊥
,外接圆直径为AB,圆心为(
,
)即(
,-
)
r2=|OC|2=
,
∴△AOB的外接圆方程为(x-
)2+(y+
)2=
.
| x2 |
| a2 |
| y2 |
| b2 |
由题得
|
所以椭圆的方程是
| x2 |
| 2 |
(2)当K存在时,设直线方程为y=K(x-1).
联立
|
设A(x1,y1),B(x2,y2)x1+ x2=
| 4k2 |
| 2k2+1 |
| 2k2-2 |
| 2k2+1 |
| OA |
| OB |
∴
| OA |
| OB |
| k2-2 |
| 2k2+1 |
令
| k2-2 |
| 2k2+1 |
| m+2 |
| 1-2m |
∴-2≤m<
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
当K不存在时,A(1,
| ||
| 2 |
| ||
| 2 |
| OA |
| OB |
| 1 |
| 2 |
综上,-2≤
| OA |
| OB |
| 1 |
| 2 |
(3)
| OA |
| OB |
∴-2
| 2 |
∴-2
| 2 |
由韦达定理知k=0或k=
| 2 |
| OA |
| OB |
当
| OA |
| OB |
当
| OA |
| OB |
| OA |
| OB |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 4 |
| 5 |
| ||
| 5 |
r2=|OC|2=
| 18 |
| 25 |
∴△AOB的外接圆方程为(x-
| 4 |
| 5 |
| ||
| 5 |
| 18 |
| 25 |
点评:本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
两圆ρ=2cosθ,ρ=2sinθ的公共部分面积是( )
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

 在港口
在港口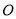 正东方
正东方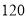 海里处,小岛
海里处,小岛 在港口
在港口 北偏东
北偏东 方向和港口
方向和港口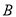 北偏西
北偏西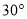 方向上,一艘科学考察船从港口O出发,沿北偏东
方向上,一艘科学考察船从港口O出发,沿北偏东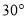 的
的 方向以每小时
方向以每小时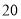 海里的速度驶离港口
海里的速度驶离港口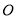 ,一艘快艇从港口B出发,以每小时
,一艘快艇从港口B出发,以每小时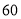 海里的速度驶向小岛
海里的速度驶向小岛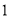 小时,问快艇驶离港口
小时,问快艇驶离港口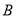 后最少要经过多少时间才能和考察船相遇?
后最少要经过多少时间才能和考察船相遇?