题目内容
在极坐标系中，圆ρ=2cosθ的圆心到直线ρcos(θ-
)=1的距离是（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点：简单曲线的极坐标方程
专题：计算题
分析：极坐标方程化为直角坐标方程，用点到直线的距离公式求出圆心到直线的距离．
解答：
解：圆ρ=2cosθ的直角坐标方程为 （x-1）2+y2=1，表示圆心在（1，0），半径等于1的圆．
直线ρcos(θ-
)=1的直角坐标方程为 x-
y-2=0，由点到直线的距离公式可得
所求的距离d=
=
，
故选C．
直线ρcos(θ-
| π |
| 3 |
| 3 |
所求的距离d=
| |1-0-2| | ||
|
| 1 |
| 2 |
故选C．
点评：本题考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，是一道基础题．
练习册系列答案
相关题目
设f（x）是定义域为R的奇函数，且在（0，+∞）上是减函数，若f（1）=0，则不等式f（x）＞0的解集是（ ）
| A、（-∞，-1）∪（1，+∞） |
| B、（-1，0）∪（0，1） |
| C、（-∞，-1）∪（0，1） |
| D、（-1，0）∪（1，+∞） |
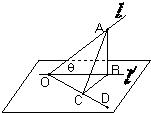如图，l是平面α的斜线，斜足是O，A是l上任意一点，AB是平面α的垂线，B是垂足，设OD是平面α内与OB不同的一条直线，AC垂直于OD于C，若直线l与平面α所成的角θ=45°，∠BOC=45°，求∠AOC的大小．两圆ρ=2cosθ，ρ=2sinθ的公共部分面积是（ ）
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
甲、乙、丙三个同学排成一排拍照，则甲排在中间的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|