题目内容
若等差数列{an}与等差数列{bn}的通项比为:
=
,{an}的前n项和记为Sn,{bn}的前n项和记为Tn,则
= .
| an |
| bn |
| 2n+1 |
| 3n+2 |
| S9 |
| T9 |
考点:等差数列的性质
专题:计算题
分析:根据在等差数列中前九项的和等于九倍的第五项,把前n项和之比写成项之比,根据所给的条件代入数字得到结果.
解答:
解:∵
=
,
∴
=
=
∵
=
∴
=
,
故答案为:
| an |
| bn |
| 2n+1 |
| 3n+2 |
∴
| a5 |
| b5 |
| 2×5+1 |
| 3×5+2 |
| 11 |
| 17 |
∵
| S9 |
| T9 |
| a5 |
| b5 |
∴
| S9 |
| T9 |
| 11 |
| 17 |
故答案为:
| 11 |
| 17 |
点评:本题考查等差数列的性质,本题解题的关键是把前n项和之比转化成成项之比,本题是一个基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
两圆ρ=2cosθ,ρ=2sinθ的公共部分面积是( )
A、
| ||||
| B、π-2 | ||||
C、
| ||||
D、
|
已知点P(x,y)在以原点为圆心的单位圆上运动,则点Q(x+y,xy)的轨迹是( )
| A、圆 | B、抛物线 | C、椭圆 | D、双曲线 |
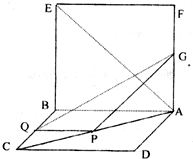 如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;
如图,在直二面角E-AB-C中,四边形ABCD和四边形ABEF都是矩形,AB=AF=4,AD=2,点P、Q、G分别是AC、BC、AF的中点;