题目内容
已知△ABC的内角A,B,C的对边分别为a,b,c,若csinC=acosB+bcosA,则△ABC的形状为( )
| A、锐角三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
考点:正弦定理
专题:解三角形
分析:已知等式利用正弦定理化简,
解答:
解:已知等式csinC=acosB+bcosA,利用正弦定理化简得:sin2C=sinAcosB+sinBcosA=sin(A+B)=sinC,
∵sinC≠0,∴sinC=1,
∴C=90°,
则△ABC为直角三角形,
故选:C.
∵sinC≠0,∴sinC=1,
∴C=90°,
则△ABC为直角三角形,
故选:C.
点评:此题考查了正弦定理,以及两角和与差的正弦函数公式,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、27 | ||
| C、30 | ||
D、
|
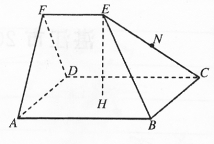 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.