题目内容
已知函数f(x)=-x2+2ax-3a.
(Ⅰ)若函数f(x)在(-∞,1)上是增函数,求实数a的取值范围;
(Ⅱ)若函数f(x)存在零点,求实数a的取值范围;
(Ⅲ)分别求出当a=1和a=2时函数f(x)在[1,3]上的最大值.
(Ⅰ)若函数f(x)在(-∞,1)上是增函数,求实数a的取值范围;
(Ⅱ)若函数f(x)存在零点,求实数a的取值范围;
(Ⅲ)分别求出当a=1和a=2时函数f(x)在[1,3]上的最大值.
考点:二次函数在闭区间上的最值,函数单调性的判断与证明,函数的零点
专题:函数的性质及应用
分析:(Ⅰ)由已知得二次函数f(x)的图象的对称轴方程为x=a,根据函数y=f(x)在(-∞,1)上是增函数,可得实数a的取值范围.
(Ⅱ)由判别式△≥0,求得实数a的取值范围.
(Ⅲ)①当a=1时,根据函数f(x)在[1,3]上是减函数,求得f(x)max的值;②当a=2时,根据函数f(x)在[1,2]上是增函数,在(2,3]上是减函数,求得f(x)max的值.
(Ⅱ)由判别式△≥0,求得实数a的取值范围.
(Ⅲ)①当a=1时,根据函数f(x)在[1,3]上是减函数,求得f(x)max的值;②当a=2时,根据函数f(x)在[1,2]上是增函数,在(2,3]上是减函数,求得f(x)max的值.
解答:
解:(Ⅰ)由已知得f(x)=-x2+2ax-3a=-(x-a)2+a2-3a,
∵函数y=f(x)在(-∞,1)上是增函数,所以a≥1,故实数a的取值范围是[1,+∞).
(Ⅱ)因为函数y=f(x)存在零点,∴△=(2a)2-4×(-1)×(-3a)≥0,即a2-3a≥0,
解得a≤0,或a≥3,故实数a的取值范围是(-∞,0]∪[3,+∞).
(Ⅲ)①当a=1时,函数f(x)=-x2+2x-3在[1,3]上是减函数,于是,f(x)max=f(1)=-2.
②当a=2时,函数f(x)=-x2+4x-6在[1,2]上是增函数,在(2,3]上是减函数,
于是,f(x)max=f(2)=-2.
∵函数y=f(x)在(-∞,1)上是增函数,所以a≥1,故实数a的取值范围是[1,+∞).
(Ⅱ)因为函数y=f(x)存在零点,∴△=(2a)2-4×(-1)×(-3a)≥0,即a2-3a≥0,
解得a≤0,或a≥3,故实数a的取值范围是(-∞,0]∪[3,+∞).
(Ⅲ)①当a=1时,函数f(x)=-x2+2x-3在[1,3]上是减函数,于是,f(x)max=f(1)=-2.
②当a=2时,函数f(x)=-x2+4x-6在[1,2]上是增函数,在(2,3]上是减函数,
于是,f(x)max=f(2)=-2.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了转化的数学思想,属基础题.

练习册系列答案
相关题目
已知△ABC的内角A,B,C的对边分别为a,b,c,若csinC=acosB+bcosA,则△ABC的形状为( )
| A、锐角三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
函数f(x)=x2+2x,x∈[-2,1]的值域是( )
| A、[0,3] |
| B、[-2,3] |
| C、[-1,0] |
| D、[-1,3] |
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的体积是( )cm3.
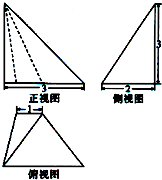

| A、4 | B、3 | C、6 | D、5 |
函数f(x)=ax2+bx+c,若f(1)<0,f(2)>0,则f(x)在(1,2)上零点的个数为( )
| A、至多有一个 |
| B、有一个或两个 |
| C、有且仅有一个 |
| D、一个也没有 |
已知向量
,
均为单位向量,若它们的夹角是60°,则|
-3
|等于( )
| a |
| b |
| a |
| b |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
若函数y=lg(x2-ax+4)的值域为R,则实数a的取值范围为( )
| A、(-4,4) |
| B、[-4,4] |
| C、(-∞,4)∪(4,+∞) |
| D、(-∞,-4]∪[4,+∞) |