题目内容
在区间（15，25]内的所有实数中随机取一个实数a，则这个实数满足17＜a＜20的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：分别计算出区间（15，25]的长度，区间（17，20）的长度，代入几何概型概率计算公式，即可得到答案．
解答：
解：由于试验的全部结果构成的区域长度为25-15=10，
构成该事件的区域长度为20-17=3，
所以概率为
．
故选：A．．
构成该事件的区域长度为20-17=3，
所以概率为
| 3 |
| 10 |
故选：A．．
点评：本题主要考查几何概型的概率计算．其中根据已知条件计算出基本事件总数对应的几何量的大小，和满足条件的几何量的大小是解答本题的关键．
练习册系列答案
相关题目
已知抛物线x2=4y上一点A的纵坐标为3，则点A与抛物线焦点的距离为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知四面体P-ABC，PA⊥平面ABC，若PA=2，AB=BC=AC=
，则该四面体的外接球的体积为（ ）
| 6 |
A、
| ||
| B、2π | ||
C、2
| ||
D、4
|
（
+
）5展开式的常数项为80，则a的值为（ ）
| x |
| a | |||
|
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
如图，在圆心角为直角的扇形OAB中，随机投入一点，则该点落入三角形区域（阴影部分）的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
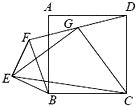如图，四边形ABCD是正方形，△BEF是等腰直角三角形，∠BEF=90°，BE=EF．连接DF，G为DF的重点，连接EG，CG，EC，求证：|
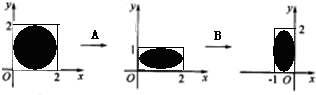二阶矩阵A，B对应的变换对圆的区域作用结果如图所示．