题目内容
已知四面体P-ABC，PA⊥平面ABC，若PA=2，AB=BC=AC=
，则该四面体的外接球的体积为（ ）
| 6 |
A、
| ||
| B、2π | ||
C、2
| ||
D、4
|
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：求出△ABC的外接圆的半径，可得四面体的外接球的半径，即可求出该四面体的外接球的体积．
解答：
解：∵AB=BC=AC=
，
∴△ABC的外接圆的半径为
，
∵PA⊥平面ABC，PA=2，
∴四面体的外接球的半径为
=
，
∴四面体的外接球的体积为
π×(
)3=4
π．
故选：D．
| 6 |
∴△ABC的外接圆的半径为
| 2 |
∵PA⊥平面ABC，PA=2，
∴四面体的外接球的半径为
| 2+1 |
| 3 |
∴四面体的外接球的体积为
| 4 |
| 3 |
| 3 |
| 3 |
故选：D．
点评：本题考查四面体的外接球的体积，考查学生的计算能力，确定四面体的外接球的半径是关键．
练习册系列答案
相关题目
如果
•
=
•
且
≠
，那么（ ）
| a |
| b |
| a |
| c |
| a |
| 0 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在棱长为4的正方体ABCD-A1B1C1D1中，E、F分别为棱AA1、D1C1上的动点，点G为正方形B1BCC1的中心．则空间四边形AEFG在该正方体各个面上的正投影所构成的图形中，面积的最大值为（ ）| A、4 | B、8 | C、12 | D、16 |
若△ABC 的三边长分别为a，b，c，面积为s．则△ABC的内切圆半径 r=
；类似的，若四面体ABCD的四个面的面积分别为s1，s2，s3，s4，体积为V，则四面体ABCD的内切球半径r为（ ）
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
有二种产品，合格率分别为0.90，0.95，各取一件进行检验，恰有一件不合格的概率为（ ）
| A、0.45 | B、0.14 |
| C、0.014 | D、0.045 |
已知|
|=3，|
|=4且向量
与
的夹角是
，则向量
在
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在区间（15，25]内的所有实数中随机取一个实数a，则这个实数满足17＜a＜20的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
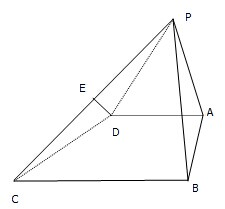如图所示，在四棱锥P-ABCD中，△PAB为正三角形，且面PAB⊥面ABCD，四边形ABCD为直角梯形，且AD∥BC，∠BCD=