题目内容
已知
,
,
是同一平面内的三个向量,其中
=(1,2).
(Ⅰ)若|
|=2
,且
∥
,求向量
;
(Ⅱ)若|
|=
,且
+2
与2
-
垂直,求
与
的夹角的正弦值.
| a |
| b |
| c |
| a |
(Ⅰ)若|
| c |
| 5 |
| c |
| a |
| c |
(Ⅱ)若|
| b |
3
| ||
| 2 |
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(I)利用向量共线定理即可得出;
(II))由
+2
与2
-
垂直,可得(
+2
)•(2
-
)=0,利用数量积的运算性质展开即可得出.
(II))由
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:(I)∵
∥
,可设
=λ
,∴|
|=|λ| |
|,2
=|λ|•
,
解得λ=±2,
∴
=2
=(2,4),或
=-2
=(-2,-4).
(II)∵
+2
与2
-
垂直,
∴(
+2
)•(2
-
)=0,
化为2
2-2
2+3
•
=0,
∴2×5-2×
+3
×
cosθ=0,
∴cosθ=
,sinθ=
,
∴
与
的夹角的正弦值
.
| c |
| a |
| c |
| a |
| c |
| a |
| 5 |
| 5 |
解得λ=±2,
∴
| c |
| a |
| c |
| a |
(II)∵
| a |
| b |
| a |
| b |
∴(
| a |
| b |
| a |
| b |
化为2
| a |
| b |
| a |
| b |
∴2×5-2×
| 45 |
| 4 |
| 5 |
3
| ||
| 2 |
∴cosθ=
| 5 |
| 9 |
2
| ||
| 9 |
∴
| a |
| b |
2
| ||
| 9 |
点评:本题考查了向量共线定理、数量积的运算性质、同角三角函数的平方关系,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
已知|
|=3,|
|=4且向量
与
的夹角是
,则向量
在
方向上的投影是( )
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
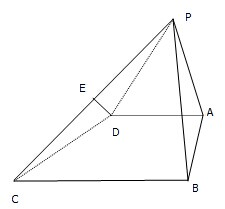 如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=
如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=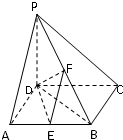 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.