题目内容
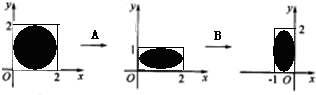 二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.
二阶矩阵A,B对应的变换对圆的区域作用结果如图所示.(Ⅰ)请写出一个满足条件的矩阵A,B;
(Ⅱ)利用(Ⅰ)的结果,计算C=BA,并求出曲线x-y-1=0在矩阵C对应的变换作用下的曲线方程.
考点:变换、矩阵的相等
专题:选作题,矩阵和变换
分析:(Ⅰ)由题意,二阶矩阵A对应的变换是横坐标不变,纵坐标的变换,二阶矩阵B对应的变换是逆时针旋转90°的旋转变换,故可求;
(2)先求得到C,设曲线x-y-1=0上任一点为(m,n),变换后的点的坐标为(x,y),从而有
=
,故m=y,n=-2x,从而可求曲线方程.
(2)先求得到C,设曲线x-y-1=0上任一点为(m,n),变换后的点的坐标为(x,y),从而有
|
|
|
解答:
解:(Ⅰ)由题意,二阶矩阵A对应的变换是横坐标不变,纵坐标变为原来一半的变换,故A=
二阶矩阵B对应的变换是逆时针旋转90°的旋转变换,故B=
…(4分)
(Ⅱ)C=BA=
=
设曲线x-y-1=0上任一点为(m,n),变换后的点的坐标为(x,y)
∵
=
∴m=y,n=-2x
∵m-n-1=0
∴2x+y-1=0
故所求曲线方程为:2x+y-1=0. …(7分)
|
二阶矩阵B对应的变换是逆时针旋转90°的旋转变换,故B=
|
(Ⅱ)C=BA=
|
|
|
设曲线x-y-1=0上任一点为(m,n),变换后的点的坐标为(x,y)
∵
|
|
|
∴m=y,n=-2x
∵m-n-1=0
∴2x+y-1=0
故所求曲线方程为:2x+y-1=0. …(7分)
点评:本题主要考查了二阶矩阵,几种特殊的矩阵变换,属于中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、D1C1上的动点,点G为正方形B1BCC1的中心.则空间四边形AEFG在该正方体各个面上的正投影所构成的图形中,面积的最大值为( )
在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、D1C1上的动点,点G为正方形B1BCC1的中心.则空间四边形AEFG在该正方体各个面上的正投影所构成的图形中,面积的最大值为( )| A、4 | B、8 | C、12 | D、16 |
在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
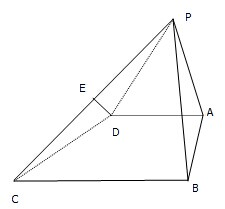 如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=
如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=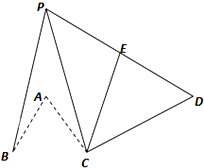 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.