题目内容
如图，在圆心角为直角的扇形OAB中，随机投入一点，则该点落入三角形区域（阴影部分）的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：计算题,概率与统计
分析：以面积为测度，利用几何概型概率公式，即可求解．
解答：
解：设半径为r，则S扇形OAB=
πr2，S△OAB=
r2，
∴所求概率为P=
=
．
故选：C．
| 1 |
| 4 |
| 1 |
| 2 |
∴所求概率为P=
| ||
|
| 2 |
| π |
故选：C．
点评：本题主要考查了几何概型，解题的关键是求阴影部分的面积，属于基础题．
练习册系列答案
相关题目
“x＞0且y＜0”是“xy＜0”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若△ABC 的三边长分别为a，b，c，面积为s．则△ABC的内切圆半径 r=
；类似的，若四面体ABCD的四个面的面积分别为s1，s2，s3，s4，体积为V，则四面体ABCD的内切球半径r为（ ）
| 2s |
| a+b+c |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知|
|=3，|
|=4且向量
与
的夹角是
，则向量
在
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
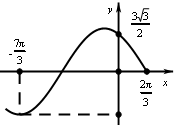已知ω＞0，-π＜φ＜π，函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（x）解析式为（ ）A、f（x）=3sin（
| ||||
B、f（x）=3sin（
| ||||
C、f（x）=3sin（
| ||||
D、f（x）=3sin（2x+
|
在区间（15，25]内的所有实数中随机取一个实数a，则这个实数满足17＜a＜20的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
