题目内容
（
+
）5展开式的常数项为80，则a的值为（ ）
| x |
| a | |||
|
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
考点：二项式定理的应用
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得展开式中的常数项的值．
解答：
解：（
+
）5展开式的通项公式为 Tr+1=
•ar•x
，
令
=0，求得r=3，可得展开式的常数项为
•a3=80，解得a=2，
故选：B．
| x |
| a | |||
|
| C | r 5 |
| 15-5r |
| 6 |
令
| 15-5r |
| 6 |
| C | 3 5 |
故选：B．
点评：本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
对于集合M，N，定义M-N={x|x∈M且x∉N}，M⊕N=（M-N）∪（N-M），设M={y|y=x2-4x，x∈R}，N={y|y=-2x，x∈R}，则M⊕N=（ ）
| A、（-4，0] |
| B、[-4，0） |
| C、（-∞，-4]∪（0，+∞） |
| D、（-∞，-4）∪[0，+∞） |
在棱长为4的正方体ABCD-A1B1C1D1中，E、F分别为棱AA1、D1C1上的动点，点G为正方形B1BCC1的中心．则空间四边形AEFG在该正方体各个面上的正投影所构成的图形中，面积的最大值为（ ）| A、4 | B、8 | C、12 | D、16 |
有二种产品，合格率分别为0.90，0.95，各取一件进行检验，恰有一件不合格的概率为（ ）
| A、0.45 | B、0.14 |
| C、0.014 | D、0.045 |
已知|
|=3，|
|=4且向量
与
的夹角是
，则向量
在
方向上的投影是（ ）
| a |
| b |
| a |
| b |
| π |
| 6 |
| a |
| b |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
“x-2＞0”是“x＞1”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
在区间（15，25]内的所有实数中随机取一个实数a，则这个实数满足17＜a＜20的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
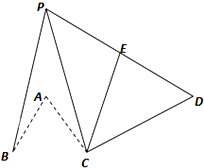在如图所示的四棱锥P-ABCD中，已知PA⊥平面ABCD，AD∥BC，∠BAD=90°，PA=AB=BC=1，AD=2，E为PD的中点．