题目内容
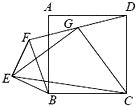 如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|
如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|| EG |
| CG |
| EG |
| CG |
考点:平面向量数量积的运算
专题:证明题,平面向量及应用
分析:以B为坐标原点,BC所在的直线为x轴,建立如图所示的直角坐标系,设A(0,1),C(1,0),D(1,1),E(p,q),F(m,n),由条件得到m=p+q,n=q-p,从而求出F、G的坐标,运用向量的模的坐标公式和向量的垂直的坐标公式,即可得证.
解答:
证明:以B为坐标原点,BC所在的直线为x轴,
建立如图所示的直角坐标系,
设A(0,1),C(1,0),D(1,1),E(p,q),F(m,n),
由于△BEF是等腰直角三角形,∠BEF=90°,BE=EF,
则
•
=-1且2(p2+q2)=m2+n2,
解得m=p+q,n=q-p,即F(p+q,q-p),
G(
,
),
故|
|2=(
)2+(
)2,
|
|2=(
)2+(
)2,
显然有|
|=|
|,
=(
,
),
=(
,
)
则
•
=
•
+
•
=0,
故
⊥
.

建立如图所示的直角坐标系,
设A(0,1),C(1,0),D(1,1),E(p,q),F(m,n),
由于△BEF是等腰直角三角形,∠BEF=90°,BE=EF,
则
| n-q |
| m-p |
| q |
| p |
解得m=p+q,n=q-p,即F(p+q,q-p),
G(
| p+q+1 |
| 2 |
| q-p+1 |
| 2 |
故|
| CG |
| p+q-1 |
| 2 |
| q-p+1 |
| 2 |
|
| EG |
| q+1-p |
| 2 |
| q+p-1 |
| 2 |
显然有|
| EG |
| CG |
| CG |
| p+q-1 |
| 2 |
| q-p+1 |
| 2 |
| EG |
| q+1-p |
| 2 |
| -q-p+1 |
| 2 |
则
| CG |
| EG |
| p+q-1 |
| 2 |
| q+1-p |
| 2 |
| q-p+1 |
| 2 |
| -q-p+1 |
| 2 |
故
| EG |
| CG |
点评:本题考查平面向量的运用,考查向量的坐标运算,向量的垂直的条件以及数量积的坐标运算和向量的模,属于中档题.

练习册系列答案
相关题目
将演绎推理:“正弦函数是奇函数,f(x)=sinx2+1是正弦函数,所以f(x)=sinx2+1是奇函数.”以上推理( )
| A、结论错误 | B、大前提错误 |
| C、小前提错误 | D、都不正确 |
有二种产品,合格率分别为0.90,0.95,各取一件进行检验,恰有一件不合格的概率为( )
| A、0.45 | B、0.14 |
| C、0.014 | D、0.045 |
“x-2>0”是“x>1”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
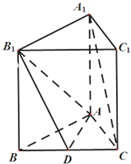 如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.
如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.