题目内容
已知函数f(x)=
x2-alnx(a>0).
(Ⅰ)若f(x)在x=2处的切线与直线2x+3y+1=0垂直,求f(x)的单调区间;
(Ⅱ)求f(x)在区间[1,e]上的最大值.
| 1 |
| 2 |
(Ⅰ)若f(x)在x=2处的切线与直线2x+3y+1=0垂直,求f(x)的单调区间;
(Ⅱ)求f(x)在区间[1,e]上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出f′(x)=
,由f(x)在x=2处的切线与直线2x+3y+1=0垂直,则f′(2)=
,a=1,此时f(x)=
x2-lnx,f′(x)=
,从而求出函数的单调区间;
(Ⅱ)由f′(x)=
,a>0及定义域为(0,+∞),令f′(x)=0,得x=
,讨论①若0<
≤1,②若1<
<e,③若
≥e从而综合得出结论.
| x2-a |
| x |
| 3 |
| 2 |
| 1 |
| 2 |
| x2-1 |
| x |
(Ⅱ)由f′(x)=
| x2-a |
| x |
| a |
| a |
| a |
| a |
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),
f′(x)=
,
由f(x)在x=2处的切线与直线2x+3y+1=0垂直,则f′(2)=
,a=1,
此时f(x)=
x2-lnx,f′(x)=
,
令f′(x)=0得x=1,
f′(x),f(x)的情况如下:
所以f(x)单调递减区间是(0,1),单调递增区间是(1,+∞).
(Ⅱ)由f′(x)=
,a>0及定义域为(0,+∞),
令f′(x)=0,得x=
.
①若0<
≤1,即0<a≤1时,在[1,e]上,f′(x)≥0,f(x)单调递增,f(x)max=f(e)=
-a,
②若1<
<e,即1<a<e2在(1,
)上,
f′(x)<0,f(x)单调递减;在(
,e)上,f′(x)>0,f(x)单调递增,
因此在[1,e]上,f(x)max=max{f(1),f(e)},
f(1)=
,f(e)=
-a,令
=
-a,解得a=
,
当1<a<
时,
-a>
,所以f(x)max=
-a;
当
≤a<e2时,
>
-a,所以f(x)max=f(1)=
.
③若
≥e,即a≥e2时,在(1,e)上,f′(x)<0,f(x)在[1,e]上单调递减,f(x)max=f(1)=
,
综上,当0<a<
时f(x)max=
-a;当a≥
时,f(x)max=
.
f′(x)=
| x2-a |
| x |
由f(x)在x=2处的切线与直线2x+3y+1=0垂直,则f′(2)=
| 3 |
| 2 |
此时f(x)=
| 1 |
| 2 |
| x2-1 |
| x |
令f′(x)=0得x=1,
f′(x),f(x)的情况如下:
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | ↗ |
(Ⅱ)由f′(x)=
| x2-a |
| x |
令f′(x)=0,得x=
| a |
①若0<
| a |
| e2 |
| 2 |
②若1<
| a |
| a |
f′(x)<0,f(x)单调递减;在(
| a |
因此在[1,e]上,f(x)max=max{f(1),f(e)},
f(1)=
| 1 |
| 2 |
| e2 |
| 2 |
| 1 |
| 2 |
| e2 |
| 2 |
| e2-1 |
| 2 |
当1<a<
| e2-1 |
| 2 |
| e2 |
| 2 |
| 1 |
| 2 |
| e2 |
| 2 |
当
| e2-1 |
| 2 |
| 1 |
| 2 |
| e2 |
| 2 |
| 1 |
| 2 |
③若
| a |
| 1 |
| 2 |
综上,当0<a<
| e2-1 |
| 2 |
| e2 |
| 2 |
| e2-1 |
| 2 |
| 1 |
| 2 |
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
相关题目
在区间(15,25]内的所有实数中随机取一个实数a,则这个实数满足17<a<20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
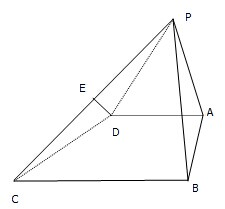 如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=
如图所示,在四棱锥P-ABCD中,△PAB为正三角形,且面PAB⊥面ABCD,四边形ABCD为直角梯形,且AD∥BC,∠BCD=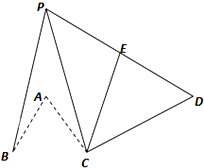 在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
在如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=AB=BC=1,AD=2,E为PD的中点.
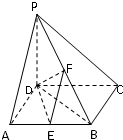 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点.