题目内容
19.已知集合A={x∈Z|(x+2)(x-1)<0},B={-2,-1},那么A∪B等于( )| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |
分析 先求出集合A,由此利用并集的定义能求出A∪B的值.
解答 解:∵B={-2,-1},
集合A={x∈Z|(x+2)(x-1)<0}={-1,0},
∴A∪B={-2,-1,0}.
故选:B.
点评 本题考查并集的求法,是基础题,解题时要认真审题,注意并集定义的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
10.设m,n是两条不同的直线,α,β是两个不同的平面,且m?α,n?β,下列命题中正确的是( )
| A. | 若α⊥β,则m⊥n | B. | 若α∥β,则m∥n | C. | 若m⊥n,则α⊥β | D. | 若n⊥α,则α⊥β |
14.已知函数f(x)=$\frac{e(x-1)}{{e}^{x}}$,若存在两对关于y轴对称的点分别再直线y=k(x+1)(k≠0)和函数y=f(x)的图象上,则实数k的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,-1)∪(-1,0) |
4.如果函数f(x)=sinωx+$\sqrt{3}$cosωx的两个相邻零点间的距离为2,那么f(1)+f(2)+f(3)+…+f(9)的值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
8.某学校为了解学生的学习、生活等情况,决定召开一次学生座谈会.此学校各年级人数情况如表:
(1)若按年级用分层抽样的方法抽取n个人,其中高二年级22人,高三年级20人,再从这n个人中随机抽取出1人,此人为高三年级的概率为$\frac{10}{33}$,求x、y的值.
(2)若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本,从这5人中任取2人,求至少有1人是男生的概率.
| 年 级 性 别 | 高一年级 | 高二年级 | 高三年级 |
| 男 | 520 | y | 400 |
| 女 | x | 610 | 600 |
(2)若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本,从这5人中任取2人,求至少有1人是男生的概率.
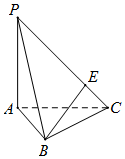 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.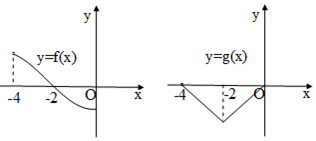 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).