题目内容
4.记a=sin1,b=sin2,c=sin3,则( )| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
分析 利用诱导公式、正弦函数的单调性即可得出.
解答 解:如图所示,
∵$\frac{π}{2}$>π-2>1>0,
∴sin2=sin(π-2)>sin1,
∵$\frac{π}{2}<π-1<3<π$,
∴sin1=sin(π-1)>sin3.
综上可得:sin2>sin1>sin3.
故选B.
点评 本题考查了诱导公式、正弦函数的单调性、直线函数的图象与性质,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
14.已知函数f(x)=$\frac{e(x-1)}{{e}^{x}}$,若存在两对关于y轴对称的点分别再直线y=k(x+1)(k≠0)和函数y=f(x)的图象上,则实数k的取值范围是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (0,1)∪(1,+∞) | D. | (-∞,-1)∪(-1,0) |
12.能推出{an}是递增数列的是( )
| A. | {an}是等差数列且$\left\{{\frac{a_n}{n}}\right\}$递增 | |
| B. | Sn是等差数列{an}的前n项和,且$\left\{{\frac{S_n}{n}}\right\}$递增 | |
| C. | {an}是等比数列,公比为q>1 | |
| D. | 等比数列{an},公比为0<q<1 |
19.函数f(x)=log3x+x-3的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
16.等边△ABC的边长为$\sqrt{5}$,则$\overrightarrow{AB}•\overrightarrow{BC}$=( )
| A. | $\frac{5}{2}$ | B. | $-\frac{5}{2}$ | C. | 5 | D. | -5 |
13.若复数z满足,(4+3i)z=|3-4i|,则z的虚部为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3}{5}$i | D. | -$\frac{4}{5}$i |
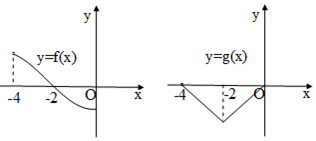 已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).
已知偶函数f(x)和奇函数g(x)的定义域都是(-4,4),且在(-4,0]上的图象如图所示,则关于x的不等式f(x)•g(x)<0的解集是(-4,-2)∪(0,2).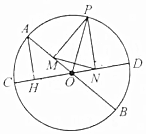 如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.
如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.