题目内容
1．
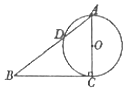如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则BD（ ）cm．| A． | 5 | B． | $\frac{16}{5}$ | C． | $\frac{6}{5}$ | D． | $\frac{17}{5}$ |
分析 由AC是⊙O的直径，AC⊥BC，可得BC是⊙O的切线．利用切割线定理可得：BC2=BD•BA即可得出．
解答 解：AB=$\sqrt{9+16}$=5，
∵AC是⊙O的直径，AC⊥BC，∴BC是⊙O的切线．
∴BC2=BD•BA，
∴42=BD•5
∴BD=$\frac{16}{5}$．
故选：B．
点评 本题考查了圆的切线的判定、勾股定理、切割线定理，属于基础题．
练习册系列答案
相关题目
19．设集合M={1，2}，N={a2}，则“a=1”是“N是M的子集”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
12．下列选项中表述正确的是（ ）
| A． | 空间中任意三点确定一个平面 | |
| B． | 直线上的两点和直线外的一点可以确定一个平面 | |
| C． | 分别在三条不同的直线上的三点确定一个平面 | |
| D． | 不共线的四点确定一个平面 |
6．变量x，y之间的一组相关数据如表所示：
若x，y之间的线性回归方程为$\widehaty$=$\widehatb$x+12.28，则$\widehatb$的值为（ ）
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A． | -0.92 | B． | -0.94 | C． | -0.96 | D． | -0.98 |
13．直三棱柱ABC-A1B1C1中，∠BAC=90°，M，N分别是A1B1，A1C1的中点，BA=CA=CC1，则BM与AN所成角的余弦值为（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{1}{10}$ | C． | $\frac{{3\sqrt{10}}}{10}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
10．已知实数a＞0，b＞0，且满足2a+3b=6，则$\frac{2}{a}$+$\frac{3}{b}$的最小值是（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{11}{3}$ | C． | $\frac{25}{6}$ | D． | 4 |