题目内容
13.直三棱柱ABC-A1B1C1中,∠BAC=90°,M,N分别是A1B1,A1C1的中点,BA=CA=CC1,则BM与AN所成角的余弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 已知ABC-A1B1C1是直三棱柱,取BC的中点0,连接A0,NM,BM,BM∥NO,BC∥NM,那么AN和NO所成角即为BM与AN所成角.求出边长,利用余弦定理求解角的大小.
解答 解:∵M,N分别是A1B1,A1C1的中点,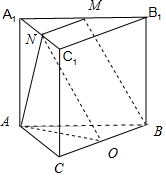
取BC的中点0,连接AO,NM,BM,
∴BM∥NO,BC∥NM且BC=2NM,
那么AN和NO所成角即为BM与AN所成角.
设BA=CA=CC1=2,∠BAC=90°,ABC-A1B1C1是直三棱柱,
∴AO=$\sqrt{2}$,AN=$\sqrt{5}$,BM=NO=$\sqrt{5}$,
∴cos∠ANO=$\frac{5+5-2}{2•\sqrt{5•\sqrt{5}}}$=$\frac{4}{5}$,
故选:A.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
1.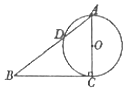 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.
 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD( )cm.| A. | 5 | B. | $\frac{16}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{17}{5}$ |
8.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
(1)画出茎叶图,由茎叶图你能获得哪些信息?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、极差、方差,并判断选谁参加比赛比较合适?
18.已知a,b∈R+,且$a+b+\frac{1}{a}+\frac{1}{b}=5$,则a+b的取值范围是( )
| A. | [1,4] | B. | [2,+∞) | C. | (2,4) | D. | (4,+∞) |
5.设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,$f(x)={({\frac{1}{2}})^x}-1$.若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | $({1,\root{4}{3}})$ | D. | $({\root{4}{3},2})$ |
3.我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1533石,验得米内夹谷,抽样取米一把,数得254粒内夹谷56粒,则这批米内夹谷约为( )
| A. | 1365石 | B. | 338石 | C. | 168石 | D. | 134石 |