题目内容
10．已知实数a＞0，b＞0，且满足2a+3b=6，则$\frac{2}{a}$+$\frac{3}{b}$的最小值是（ ）| A． | $\frac{8}{3}$ | B． | $\frac{11}{3}$ | C． | $\frac{25}{6}$ | D． | 4 |
分析 利用“乘1法”与基本不等式的性质即可得出．
解答 解：∵实数a＞0，b＞0，且满足2a+3b=6，
则$\frac{2}{a}$+$\frac{3}{b}$=$\frac{1}{6}$（2a+3b）$（\frac{2}{a}+\frac{3}{b}）$=$\frac{1}{6}$$（13+\frac{6b}{a}+\frac{6a}{b}）$≥$\frac{1}{6}（13+6×2\sqrt{\frac{b}{a}×\frac{a}{b}}）$=$\frac{25}{6}$，当且仅当b=a=$\frac{6}{5}$．
故选：C．
点评 本题考查了“乘1法”与基本不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
8．已知cos（x-$\frac{π}{4}$）=-$\frac{1}{3}$（$\frac{5π}{4}$＜x＜$\frac{7π}{4}$），则sinx-cos2x=（ ）
| A． | $\frac{5\sqrt{2}-12}{18}$ | B． | $\frac{-4\sqrt{2}-7}{9}$ | C． | $\frac{4-7\sqrt{2}}{9}$ | D． | $\frac{-4-7\sqrt{2}}{9}$ |
1．
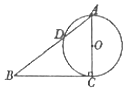如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则BD（ ）cm．
如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则BD（ ）cm．| A． | 5 | B． | $\frac{16}{5}$ | C． | $\frac{6}{5}$ | D． | $\frac{17}{5}$ |
18．已知a，b∈R+，且$a+b+\frac{1}{a}+\frac{1}{b}=5$，则a+b的取值范围是（ ）
| A． | [1，4] | B． | [2，+∞） | C． | （2，4） | D． | （4，+∞） |
5．设f（x）是定义在R上的偶函数，对任意的x∈R，都有f（x-2）=f（x+2），且当x∈[-2，0]时，$f（x）={（{\frac{1}{2}}）^x}-1$．若在区间（-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）恰有3个不同的实数根，则实数a的取值范围是（ ）
| A． | （1，2） | B． | （2，+∞） | C． | $（{1，\root{4}{3}}）$ | D． | $（{\root{4}{3}，2}）$ |
某学校1800名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13，14]，第二组[14，15），第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
20．若x，y是正数，且$\frac{1}{x}+\frac{4}{y}=1$，则x+y有（ ）
| A． | 最小值9 | B． | 最大值9 | C． | 最小值$5+2\sqrt{2}$ | D． | 最大值$5+2\sqrt{2}$ |