题目内容

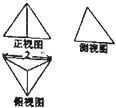
如图是各条棱长均为2的正四面体的三视图，则正视图三角形的面积为（　　）
A、
3
B、
2
3
6
C、2
3
D、
4
3
6
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：三视图中长对正，高对齐，宽相等，由题意确定正视图三角形的底边长与高．
解答： 解：∵是各条棱长均为2的正四面体的三视图，
∴正视图的底边长为2，
高为
22-(2•
3
2
•
2
3
)2
=
2
6
3
，
则S=
1
2
×2×
2
6
3
=
2
6
3
．
故选B．
点评：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．
练习册系列答案
相关题目
已知命题p：关于x的不等式ax＞1，（a＞0，a≠1）的解集是{x|x＜0}，命题q：函数y=lg（x2-x+a）的定义域为R，若p∨q为真p∧q为假，求实数a的取值范围．
在复平面内，复数
3-i
2+i
（i为虚数单位）对应的点在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
△ABC的内角A，B，C的对边a，b，c成等差数列，且5sinA=7sinB，则角A=（　　）
A、
π
3
B、
2π
3
C、
3π
4
D、
5π
6
在?ABCD中，O是对角线AC与BD的交点，E是BC边的中点，连接DE交AC于点F．已知
AB
=
a
，
AD
=
b
，则
OF
=
 
（用
a
和
b
表示）
已知函数f（x）=lnx，g（x）=ex
（1）若函数φ（x）=-x+f（-x），当x∈[-e，0）时，求φ（x）的值域．
（2）设直线l为函数f（x）的图象上一点A（x0，f（x0））处切线．证明：在区间（1，+∞）上存在唯一的x0使得直线l与曲线y=g（x）相切．
已知椭圆C：
x2
a2
+
y2
b2
=1，的离心率e=
5
5
，以两个焦点F1，F2和短轴的两个端点B1，B2为顶点的四边形F1B1F2B2的面积为4．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设过点P（4，0）的直线l与椭圆C交于A，B两点，若线段AB的中点落在F1B1F2B2四边形内（含边界），求直线l斜率的取值范围．
如图，在直角梯形ABCD中，AB=2CD=2AD，AD⊥AB，将△ADC沿AC这起，使平面ADC⊥平面ABC，得到几何体D-ABC．

（Ⅰ）求证：BC⊥AD；
（Ⅱ）点M是线段DB上的一点，当二面角M-AC-D的大小为时
π
3
时，求
DM
NB
的值．
己知命题p：方程
x2
5-k
+
y2
k+1
=1表示焦点在y轴上的椭圆，命题q：方程
x2
5-k
+
y2
k+1
=1表示双曲线．如果p∨q为真，p∧q为假，求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网