题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 5 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点P(4,0)的直线l与椭圆C交于A,B两点,若线段AB的中点落在F1B1F2B2四边形内(含边界),求直线l斜率的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意得
,由此能求出椭圆方程.
(2)设直线l的方程为y=k(x-4),由
,得(5k2+4)x2-40k2x+80k2-20=0,由此利用根的判别式、直线方程的性质,结合已知条件,能求出直线l斜率的取值范围.
|
(2)设直线l的方程为y=k(x-4),由
|
解答:
解:(1)由题意得
,
解得a=
,b=2,c=1,
∴椭圆方程为:
+
=1.
(2)设直线l的方程为y=k(x-4),
由
,得(5k2+4)x2-40k2x+80k2-20=0,
∵直线l与椭圆交于A,B两点,
∴△=1600k4-4(5k2+4)(80k2-20)>0,
解得-
<k<
,①
设A(x1,y1),B(x2,y2),AB中点M(x0,y0),则x1+x2=
,
∴x0=
≥0,
∴点M在y轴右侧,
直线B2F2方程为y=-2x+2,直线B1F2的方程为y=2x-2,
要使点M在四边形内部,(包含边界),
则
,
∴
,
化简,得
,
解得
≤k≤
,②
由①②,得:
≤k≤
.
|
解得a=
| 5 |
∴椭圆方程为:
| x2 |
| 5 |
| y2 |
| 4 |
(2)设直线l的方程为y=k(x-4),
由
|
∵直线l与椭圆交于A,B两点,
∴△=1600k4-4(5k2+4)(80k2-20)>0,
解得-
2
| ||
| 11 |
2
| ||
| 11 |
设A(x1,y1),B(x2,y2),AB中点M(x0,y0),则x1+x2=
| 40k2 |
| 5k2+4 |
∴x0=
| 20k2 |
| 5k2+4 |
∴点M在y轴右侧,
直线B2F2方程为y=-2x+2,直线B1F2的方程为y=2x-2,
要使点M在四边形内部,(包含边界),
则
|
∴
|
化简,得
|
解得
4-2
| ||
| 15 |
-4+2
| ||
| 15 |
由①②,得:
4-2
| ||
| 15 |
-4+2
| ||
| 15 |
点评:本题考查椭圆方程的求法,考查直线的斜率的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
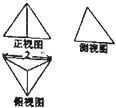
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知实数a,b满足1003a+1004b=2006b,997a+1009b=2007a,则a与b的大小关系为( )
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
已知函数f(x)=sin(x+ϕ)+cos(x+ϕ)为偶函数,则ϕ的一个取值为( )
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
将7个红球,6个白球(小球只有颜色的区别)放入5个不同盒子,要求每个盒子中至少红球、白球各一个,则不同的放法共有( )
| A、20种 | B、25种 |
| C、45种 | D、75种 |