题目内容
△ABC的内角A,B,C的对边a,b,c成等差数列,且5sinA=7sinB,则角A=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:余弦定理的应用,正弦定理
专题:解三角形
分析:由a,b,c成等差数列,利用等差数列的性质得到2b=a+c,利用正弦定理化简5sinA=7sinB,表示出a与c,利用余弦定理表示出cosA,把三边长代入求出cosA的值,即可确定出A的度数.
解答:
解:∵a,b,c成等差数列,
∴2b=a+c①,
由正弦定理化简5sinA=7sinB,得:5a=7b,即a=
b②,
②代入①得:c=
b,
∴cosA=
=
=-
,
则A=
.
故选:B.
∴2b=a+c①,
由正弦定理化简5sinA=7sinB,得:5a=7b,即a=
| 7 |
| 5 |
②代入①得:c=
| 3 |
| 5 |
∴cosA=
| b2+c2-a2 |
| 2bc |
b2+
| ||||
|
| 1 |
| 2 |
则A=
| 2π |
| 3 |
故选:B.
点评:此题考查了正弦定理,余弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
如图是各条棱长均为2的正四面体的三视图,则正视图三角形的面积为( )
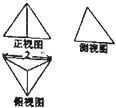

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|

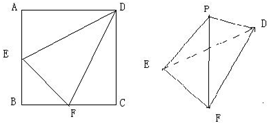 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC